Mögliche Arbeitsblätter 1-10

Arbeitsblatt 1

Aufgabe 1:

Welche Systemgrößen und welche Wechselwirkungen zwischen ihnen charakterisieren das (weitgehend abgeschlossene) Ökosystem eines Aquariums? Stelle die Ergebnisse Deiner Überlegungen in Form eines "Wirkungsgefüges" graphisch dar!

Aufgabe 2:

Versuche, das in der Aufgabe 1 erstellte qualitative Modell soweit wie möglich zu vereinfachen. Auf welche Systemgrößen und auf welche Wechselwirkungen zwischen ihnen könnte man Deiner Meinung nach vielleicht verzichten, wenn es darum geht, Ursachen der unerwünschten Veralgung und Möglichkeiten ihrer Verhinderung zu untersuchen?

Arbeitsblatt 2

Aufgabe 3:

Stelle Dir - völlig unrealistisch - einen unbegrenzt großen mit Wasser gefüllten Behälter als "Baukasten" für das Aquarium vor. In dem Wasser sollen für die nun einzusetzenden Wasserpflanzen immer optimale Bedingungen herrschen, so daß das Pflanzenwachstum immer konstant 10% der bereits vorhandenen Pflanzenmenge betragen soll. Erstelle mit Hilfe des Programms DYNASYS ein entsprechendes quantitatives Modell! Benutze dazu bei Bedarf die "Kurzinformation zum Aufbau und zur Erstellung von DYNASYS-Modellen"! Speichere das Modell unter dem Namen "pflanz1.dyn"!

Zum Aufbau und zur Erstellung von DYNASYS-Modellen

DYNASYS-Modelle bestehen nur aus folgenden vier Arten von Objekten:

   Zustandsgrößen

Zustandsgrößen sind diejenigen Modell-Größen, die den Zustand des betrachteten Systems definieren, und die sich im Laufe der Zeit durch Zuflüsse oder Abflüsse (s.u.) ändern.

   Zuflüsse und Abflüsse mit Ventilen (Änderungsraten)

Eine Zustandsgröße in einem dynamischen System kann man sich als eine mengenartige Größe vorstellen. Damit sich diese Größe verändert, muß etwas in die Zustandsgröße hineinfließen oder wieder herausflieáen. Der Fluß selbst wird durch ein Ventil geregelt. Solche Ventile werden bei dynamischen Systemen auch als Flußgrößen (Zuflüsse bzw. Abflüsse) oder Änderungsraten bezeichnet, sie geben an, um wieviel sich die Zustandsgröße pro gewählter Zeiteinheit verändert.

Der Fluß kann entweder aus einer anderen Zustandsgröße oder aus einer beliebigen Quelle stammen und zu einer zweiten Zustandsgröße oder einer Senke fließen. Im Flußdiagramm werden Senken und Quellen als Wolke dargestellt.

  Zwischengrößen, exogene Größen, Parameter

Unter Zwischengrößen verstehen wir Größen, die sich zwar im Laufe der Zeit verändern, die aber ständig aus dem Systemzustand, also aus den Zustandsgrößen, berechenbar sind.

Exogene Größen sind Veränderliche, die ein System beeinflussen, auf die das System selbst aber keinen Einfluß nehmen kann. Dazu gehören insbesondere auch Tabellenfunktionen.

Parameter sind Größen, die über die Beobachtungszeit konstant bleiben.

Zwischengrößen und exogene Größen werden in DYNASYS durch schwarze, Parameter durch rote Kreissymbole dargestellt.

  Wirkungspfeile

Wirkungen oder Informationen werden in Flußdiagrammen durch dünne Pfeile dargestellt. Dabei bedeutet ein Pfeil von Objekt A auf B "A wirkt auf B".

Aus diesen vier Arten von Objekten sind DYNASYS-Modelle denkbar einfach zu erstellen:

Im ersten Schritt wird mit Hilfe des "Modelleditors" das qualitative Modell erstellt. Es setzt sich zusammen aus:

1. benannten Zustandsgrößen,
2. Zuflüssen und Abflüssen mit benannten Ventilen (Änderungsraten),
3. benannten Zwischengrößen, exogenen Größen und Parametern,
4. Wirkungspfeilen.

Im zweiten Schritt wird - wieder mit Hilfe des "Modelleditors" - das bisher nur qualitative Modell durch Zuweisung von Werten und Formeln zum quantitativen Modell erweitert:

1. Startwerte für Zustandsgrößen,
2. Formeln für Ventile und Zwischengrößen; diese Formeln enthalten alle durch Wirkungspfeile mit den jeweiligen Ventilen bzw. Zwischengrößen verknüpften Objekte;
3. Tabellenfunktionen bzw. Konstanten für exogene Größen und Parameter.

Im Hintergrund, d.h. für den Benutzer unsichtbar, werden dadurch die für die Berechnung von Simulationen notwendigen Modellgleichungen erzeugt.

Arbeitsblatt 3

Aufgabe 4:

Lasse Dir vom Programm DYNASYS ein "Zeitdiagramm" für die zukünftige Entwicklung der Wasserpflanzen zeigen!

Dazu mußt Du zunächst unter der Option "Numerik" das gewünschte Rechenverfahren sachgerecht einstellen. DYNASYS stellt zwei Rechenverfahren zur Verfügung: das (einfache) Euler-Cauchy-Verfahren für diskrete und hinreichend kurze Prognosezeiträume sowie das Runge-Kutta-Verfahren (4. Ordnung) für kontinuierliche Systeme bzw. längere Prognosezeiträume (vgl.: Zweiter Mathematischen Exkurs: "Mathematische Verfahren zur Ermittlung von Prognosewerten").

Da Pflanzen nicht sprunghaft (=diskret), sondern stetig wachsen, handelt es sich hier um ein kontinuierliches System, so daß das Rechenverfahren "Runge-Kutta" eingestellt werden muß. Um dabei die Rechenfehler möglichst klein zu halten, sollten die betrachteten Zeitintervalle hinreichend klein sein; empfehlenswert ist hier die Einstellung dt=0,1 .

Arbeitsblatt 4

Aufgabe 5:

Warum wäre für ein echtes Aquarium ein unbegrenztes exponentielles Wachstum der Wasserpflanzenmenge unrealistisch?
Gibt es Faktoren, die das Wachstum der Wasserpflanzen auch dann begrenzen würden, wenn bezüglich ihrer Nährstoffversorgung stets optimale Bedingungen herrschen würden?
Wie könnte man eine solche Begrenzung des exponentiellen Wachstums mathematisch realisieren?

Aufgabe 6:

Verbessere mit Hilfe Deiner Lehrerin bzw. Deines Lehrers das Modell in diesem Sinne, speichere es unter dem Namen "pflanz2.dyn", und lasse Dir dann vom Programm DYNASYS die aufgrund des neuen Modells zu erwartende Entwicklung der Wasserpflanzenmenge zeigen!

Arbeitsblatt 5

Aufgabe 7:

Pflanzen wachsen nicht nur, sondern es sterben ständig auch Pflanzen(teile) ab.
Erweitere das Modell in diesem Sinne, speichere es unter dem Namen "pflanz3.dyn", und lasse Dir vom Programm DYNASYS wieder ein Zeitdiagramm zur zukünftigen Entwicklung der Wasserpflanzenmenge zeigen!
Wie wirkt sich die Modell-Änderung auf das Wachstum der Wasserpflanzen aus?

Aufgabe 8:

Wasserpflanzen ernähren sich von im Wasser gelösten Nährsalzen. Andererseits werden die in abgestorbenen Pflanzenresten gebundenen Nährsalze wieder frei und stehen erneut zur Ernährung von Wasserpflanzen zur Verfügung.
Baue das Wasserpflanzen-Modell in diesem Sinne um, speichere das neue Modell unter dem Namen "pflanz4.dyn", und lasse Dir vom Programm DYNASYS wieder ein Zeitdiagramm zur zukünftigen Entwicklung der Wasserpflanzenmenge zeigen!
Wie wirkt sich diese Modell-Änderung auf das Wachstum der Wasserpflanzen aus?

Aufgabe 9:

Versuche, das mit dem Modell aus Aufgabe 8 erzielte unsinnige Simulationsergebnis zu erklären!
Kannst Du einen "Denkfehler" bei der Modellbildung erkennen?

Arbeitsblatt 6

In dem bisher betrachteten Modell wachsen - fälschlicherweise - die Wasserpflanzen unabhängig von den jeweils vorhandenen Nährsalz-Ressourcen. Diesen Fehler gilt es nun zu korrigieren.

Dazu muß das Modell erweitert werden zu einem "Modell des Ressourcengesteuerten Wachstums" .

Aufgabe 10:

Informiere Dich über die ökologische Potenz von Wasserpflanzen gegenüber im Wasser gelösten Nährsalzen und baue diese mittels einer Tabellenfunktion in das Wasserpflanzen-Modell ein.
Speichere das neue Modell unter dem Namen "pflanz5.dyn"!
Welches Simulationsergebnis erhältst Du jetzt?

Arbeitsblatt 7

Die Entwicklung und Untersuchung eines analogen Algenmodells kann sowohl als selbständige Übertragung des Wasserpflanzenmodells durch die Schülerinnen und Schüler erfolgen (diesen - allerdings zeitaufwendigeren - Weg schlagen wir vor) als auch in arbeitsteiliger Gruppenarbeit zeitgleich mit der Entwicklung des Wasserpflanzenmodells.

Aufgabe 11:

Entwickle - analog zu dem Wasserpflanzenmodell - ein "Modell des Ressourcengesteueten Wachstums" für Algen und experimentiere damit!

Arbeitsblatt 8

Die Erörterung des nun zu entwickelnden Modells macht v.a. die Dynamik zwischenartlicher Konkurrenz um Ressourcen zum unterrichtlichen Gegenstand.

Aufgabe 12:

In dem Modellaquarium soll es als Biomasse neben den Wasserpflanzen auch Algen geben. Daher müssen nun die beiden Teilmodelle (Wasserpflanzenmodell und Algenmodell) zu einem neuen Modell zusammengefügt werden. Dabei können die Mengenangaben für Wasserpflanzen, Algen und Nährsalze als Werte mit der gemeinsamen Einheit "Algeneinheiten der Gattung Chlorella" aufgefaßt werden.

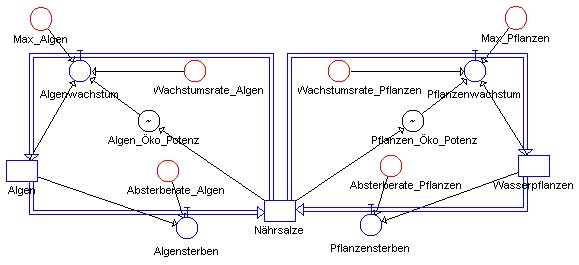
Aus diesen Überlegungen könnte sich das unten (bzw. in der Datei "algpfla.dyn") angegebene Modell ergeben.

• Experimentiere mit diesem Modell im Hinblick auf die Frage, ob und gegebenenfalls bei welcher Nährsalzmenge Algen und Wasserpflanzen langfristig in dem Modellaquarium koexistieren können, oder ob stets eine Art die andere "niederkonkurriert"! Variiere dazu nur die jeweils vorhandene Nährsalzmenge und lasse die übrigen Parameter unverändert. (Man nennt das eine "ceteris-paribus-Analyse".) Bestimme gegebenenfalls das Niveau des "Fließgleichgewichts"!
• Untersuche mit Hilfe weiterer Simulationen die Frage, was sich an dem bisher erzielten Ergebnis ändert, wenn man die Startwerte für Nährsalze, Wasserpflanzen und Algen und/oder die Grenzwerte "Max_Pflanzen" und "Max_Algen" ändert und/oder an den beiden Tabellenfunktionen zu den "ökologischen Potenzen gegenüber Nährsalzen" quantitative (jedoch keine qualitativen) Änderungen vornimmt.

Zustandsgleichungen

Nährsalze.neu <-- Nährsalze.alt
                         + dt*(Algensterben+Pflanzensterben-Pflanzenwachstum-Algenwachstum)
Startwert Nährsalze = 300000
Wasserpflanzen.neu <-- Wasserpflanzen.alt + dt*(Pflanzenwachstum-Pflanzensterben)
Startwert Wasserpflanzen = 1000
Algen.neu <-- Algen.alt + dt*(Algenwachstum-Algensterben)
Startwert Algen = 10

Zustandsänderungen

Pflanzenwachstum = Wasserpflanzen * Wachstumsrate_Pflanzen
                              * Pflanzen_Öko_Potenz*(1-Wasserpflanzen/Max_Pflanzen)
Algenwachstum = Algen * Algen_Öko_Potenz
                              * Wachstumsrate_Algen*(1-Algen/Max_Algen)
Algensterben = Algen*Absterberate_Algen
Pflanzensterben = Wasserpflanzen*Absterberate_Pflanzen

Konstanten

Max_Algen = 10000000
Max_Pflanzen = 10000000
Wachstumsrate_Algen = 1
Wachstumsrate_Pflanzen = 0,1
Absterberate_Pflanzen = 0,01
Absterberate_Algen = 0,1

Zwischenwerte

Algen_Öko_Potenz = Tabelle(Nährsalze)
((0.00;0.00)(200000.00;0.00)(400000.00;1.00)(600000.00;1.00)
(800000.00;1.00)(1000000.00;1.00)(1200000.00;1.00)(1400000.00;0.95)
(1600000.00;0.50)(1800000.00;0.20)(2000000.00;0.20))

Pflanzen_Öko_Potenz = Tabelle(Nährsalze)
((0.00;0.00)(200000.00;1.00)(400000.00;1.00)(600000.00;0.00)
(800000.00;0.00)(1000000.00;0.00)(1200000.00;0.00)(1400000.00;0.00)
(1600000.00;0.00)(1800000.00;0.00)(2000000.00;0.00))

Arbeitsblatt 9

Aufgabe 13:

Um das Modellaquarium wirklich zu einem virtuellen Aquarium zu machen, müssen jetzt natürlich noch Fische eingesetzt werden. Diese müssen regelmäßig mit einer gewissen Futtermenge (z.B. = 5000 je Fisch) versorgt werden und scheiden dann eine entsprechende Menge Kot (z.B. = Futter_je_Fisch*Fischzahl) aus, der die im Wasser gelöste Nährsalzmenge vergrößert. Erweitere das Modell in diesem Sinne und speichere es unter dem Namen "aquarium.dyn"!

Aufgabe 14:

Untersuche mit diesem Modell-Aquarium der Datei "aquarium.dyn" und mit Hilfe entsprechender Simulationen z.B. folgende Fragen:

• Wieviele Wasserpflanzen und wieviele Fische sollte man in das Modell-Aquarium einsetzen?
• Wie wirkt sich eine Erhöhung der Futtermenge aus?
• Kann man durch eine "optimale" Kombination aus Pflanzenzahl, Fischzahl und Futtermenge eine "Veralgung" vermeiden, also in dem Aquarium ein "ökologisches Gleichgewicht" herstellen?
• Was ändert sich an den bisher erzielten Ergebnissen, wenn man die Startwerte für Nährsalze, Wasserpflanzen und Algen und / oder die Grenzwerte "Max_Pflanzen" und "Max_Algen" ändert und / oder an den beiden Tabellenfunktionen zu den "ökologischen Potenzen gegenüber Nährsalzen" quantitative (jedoch keine qualitativen) Änderungen vornimmt?

Arbeitsblatt 10

Aufgabe 15:

Welche Fehlerquellen bergen Modellbildungsprozesse und (Computer-)Simulationen wie die im Verlauf dieser Unterrichtseinheit durchgeführten?

Welche Chancen und welche Gefahren sind mit ihnen verbunden?

©   Helmut Kohorst   &  Philipp Portscheller   01.08.1996

[Zurück zum Inhaltsverzeichnis]