Zweiter Mathematischer Exkurs: Math. Verfahren zur Ermittlung von Prognosewerten

Zweiter Mathematischer Exkurs:

Mathematische Verfahren zur Ermittlung von Prognosewerten

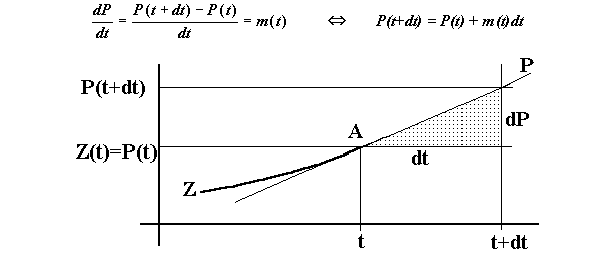
Von einer Zustandsgröße Z seien bekannt:

ihre bisherige Entwicklung bis zum Zeitpunkt t , mindestens aber ihr Wert Z(t) zu diesem Zeitpunkt t , d.h. der Punkt A(t;Z(t)).
die momentane Änderungsrate (Steigung) m=m(t) zu diesem Zeitpunkt t .

Gesucht ist nun ein Prognosewert P(t+dt) für den tatsächlichen Wert Z(t+dt) nach einer gewissen Zeitspanne dt.

Aus den obigen Angaben ( Punkt A und Steigung m ) läßt sich mit Hilfe des Steigungsdreiecks eine lineare Funktion P ermitteln, denn es ist (vgl. die folgende Skizze)

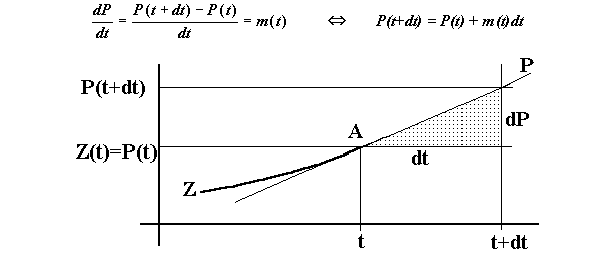
Euler-Verfahren 1

Diese lineare Funktion P läßt sich interpretieren als "Lineare Fortsetzung" ²⁾ der Funktion Z vom Zeitpunkt t bis zum Zeitpunkt t+dt.

In all den Fällen, in denen der Graph von Z im betrachteten Zeitintervall dt nur wenig von einer Geraden abweicht, stellt der nach dem obigen Euler-Cauchy-Verfahren ermittelte Wert P(t+dt) einen brauchbaren Prognosewert für den vorherzusagenden Wert Z(t+dt) dar, denn in diesen Fällen gilt:

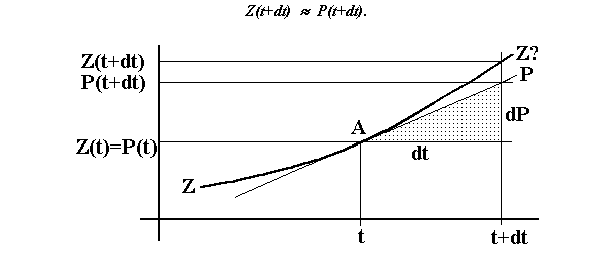
Euler-Verfahren 2

Unglücklicherweise braucht dies nicht so zu sein, wie z.B. die folgende Skizze lehrt:

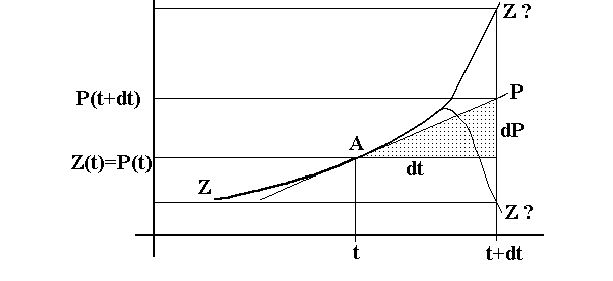
Euler-Verfahren 3

Man versucht, den dabei auftretenden Verfahrensfehler ggf. durch eine Verkleinerung des Zeitintervalls dt zu vermindern. Dies erkauft man jedoch i.a. damit, daß dann bei einer größeren Zahl von Rechenschritten (Iterationsschritten) bis zum Erreichen der vorgewählten "Prognosen-Endzeit" größere Rundungsfehler auftreten können.

Man kann also Fehler prinzipiell nicht vermeiden, und es bleibt obendrein unklar, in welcher Weise Verfahrens- und Rechenfehler den Gesamtfehler vergrößernd oder verkleinernd beeinflussen. Es ist vielmehr durchaus möglich, daß sich die Fehler bis zu ersichtlich unsinnigen Rechenergebnissen verstärken. Dies gilt in besonderem Maße für periodische Abläufe, so daß hier leicht der Eindruck eines chaotischen Verhaltens entstehen kann, obwohl dieses in der Realität gar nicht vorliegt.

Dennoch bietet das Euler-Cauchy-Verfahren bei diskreten Systemen und hinreichend kurzen Prognosezeiträumen meist eine ausreichende Genauigkeit.

Für kontinuierliche Systeme bzw. längere Prognosezeiträume reicht die mit dem Euler-Cauchy-Verfahren erzielbare Genauigkeit allerdings i.d.R. nicht aus. Hier bedient man sich des deutlich aufwendigeren, aber auch genaueren Runge-Kutta-Verfahrens, das mit mehreren Stützstellen im Zeitintervall dt arbeitet und deren Einfluß auf den Prognosewert auch noch unterschiedlich gewichtet.

Dieses Verfahren soll hier nicht näher dargestellt werden, da es das Verständnisvermögen von Schülerinnen und Schülern der Sek.I und insbesondere der 7.-9. Klasse deutlich übersteigt. Da die in diesem Unterrichtsprojekt zu untersuchenden Systeme seine Anwendung dennoch notwendig machen, muß es m.E. (zumindest in der Sek.I) wohl oder übel als "black box" benutzt werden.

Anmerkung 2):
Mathematisch ausgedrückt: Die Prognose-Funktion P ist die Tangentenfunktion zur (differenzierbaren) Funktion Z im Zeitpunkt t.
Eine solche mathematische Ausdrucks- und Schreibweise ist natürlich für Schülerinnen und Schüler zumindest der Sek.I noch nicht verständlich und sollte deswegen auch in deren Unterricht unterbleiben.

[Zurück zum Inhaltsverzeichnis]