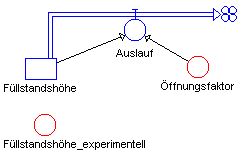
Auslauf eines Wassergefäßes (wassgef.dyn)
[Graphen]
[Unterrichtliche Anregungen] |
|
Gegeben sei ein mit einer Flüssigkeit gefülltes
zylindrisches Gefäß. An seinem Boden befinde sich ein kleines
Loch, durch das diese Flüssigkeit ausströmen kann. Das Loch möge
so klein sein, daß sich eine (weitgehend) laminare Strömung einstellen
kann. Gefragt ist der zeitliche Verlauf der Füllstandshöhe, wenn
der Behälter, anfangs bis zu einer gewissen Marke gefüllt, sich
zu leeren beginnt. Da von einem zylindrischen Gefäß ausgegangen
wird (vasenähnliche Gefäße oder andere "pathologische" Formen
darf man ruhigen Gewissens den Mathematikern zur Berechnung überlassen),
kann man statt der zeitlichen Veränderung des Füllstands
gleichermaßen auch die zeitliche Veränderung des
Flüssigkeitsvolumens untersuchen. |
für die Schule eine induktive Lösung |
|
Die Lösung dieses Problems ist rein deduktiv möglich
(Lösung: Die zeitliche Änderung des Flüssigkeitsstands ist
proportional zur Wurzel aus dem jeweiligen Flüssigkeitsstand), jedoch
in der Sekundarstufe nicht durchführbar, so daß hier "nur" der
induktive Weg gewählt werden kann (Vorteil: man kann hier den stattfindenden
Modellbildungsprozeß besonders gut verdeutlichen). Beim Auslauf der
Flüssigkeit handelt es sich also nicht, wie man gelegentlich lesen kann,
um einen exponentiell verlaufenden Vorgang, der prinzipiell erst nach unendlich
langer Zeit abgeschlossen wäre. Vielmehr folgt aus dem quadratischen
Zusammenhang zwischen der Füllstandshöhe und der Zeit eine endliche
(begrenzte) Zeitdauer bis zum völligen Auslauf der Flüssigkeit. |