|
|
|
Softwarereport |
Das grundsätzliche Problem
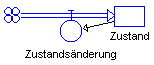
Zustandsgleichung
Zustand.neu <-- Zustand.alt + dt*(Zuwachs)
Startwert Zustand = 1
Zustandsänderung
Zuwachs = Zustand
|
|
Wechselwirkende Systeme bestehen aus einer mehr oder weniger
großen Anzahl von Variablen, die aufeinander in gleicher oder
unterschiedlicher Weise einwirken. Mathematisch lassen sich solche Systeme
als ein Satz von Differentialgleichungen oder Differenzengleichungen modellieren,
die sich in der Regel nur numerisch über iterative Prozesse lösen
lassen. Der dazu erforderliche repetetive Rechenaufwand legt die Verwendung
eines Copmputers nahe. |
Schnell, nah der Wissenschaft, aber fern den auch
Interessierten
z.B. Dynamos II
|
|
Gemeint sind formelorientierte Modellbildungswerkzeuge,
die Wirkungsbeziehungen der Modellgrößen untereinander als
Differenzengleichungen beschreiben und als Text in einer -häufig an
Pascal angelehnten- Programmiersprache eingegeben werden müssen. Iteration
und graphische Ausgabe der Ergebnisse werden dann vomWerkzeug selbständig
durchgeführt. Doch können formelorientierte Modellbildungswerkzeuge
nur zum Einsatz in der Schule kommen, wenn die mathematischen Grundlagen
der Modellbildung und Simulation explizit Thema waren, also allenfalls in
der Mathematik und der Physik der Sekundarstufe II. |
Tabellenkalkulationen, z.B. Excel und viele andere
dazu umfassend mit vielen Unterrichtsbeispielen:
Rainer Stieglitz: Systemorientierte Modellbildung im
fächerübergreifenden Unterricht. Landesinstitut für Schule
und Weiterbildung (Hg.). Soest 1994.
|
|
Auch Tabellenkalkulationen, die eine graphische Verarbeitung
der Daten unterstützen, lassen sich als Werkzeug zur Modellierung und
Simulation dynamischer Systeme nutzen. Als Standardwerkzeuge sind sie
Schülerinnen und Schüler bekannt. Zudem sind sie flexibel einsetzbar,
wenn das modellierte System nicht angemessen durch ein Wirkungsnetz mit Zustands-
und Änderungsgrößen beschrieben werden kann oder wenn eine
große Anzahl von Zustandsgrößen in einer Matrix organsiert
werden soll. Doch ihre Grenze ist klar: Nutzer sehen erst einmal keine für
sie faßbaren Modelle, sondern tabellarische Darstellungen, bei denen
die Bezüge der Sytemkomponenten in Formeln verborgen sind, die
Tabellenspalten miteinander verbinden. |
Anschaulich: Graphische Modellbildungswerkzeuge
 Modellbildungssoftware
im ‹berblick |
|
Mit Hilfe graphischer Modellbildungswerkzeuge ist es
möglich, auch ohne Kenntnisse von Differentialgleichungen und einer
Programmiersprache und zunächst unter Verzicht auf in Formeln gegossene
Bezüge Simulationsmodelle am Bildschirm zu konstruieren. Dabei wird
das Modell interaktiv als Wirkungsnetz am Bildschirm erzeugt, indem Symbole
für die Elemente Zustandsgrößen,
Änderungsgrößen, Funktionen und Konstanten einer Palette
entnommen und mittels 'drag and drop' mit der Maus auf dem Bildschirm
verknüpft werden. Anwender können sich ganz darauf konzentrieren,
ein qualitatives Modell im Wirkungsnetz zu entwickeln. Erst in einem zweiten
Schritt werden per Mausklick die Symbole geöffnet, die Größen
parametrisiert bzw. ihre Wechselwirkung in Formeln gefaßt.
Simulationsläufe lassen sich in Tabellen, Zeit- oder Phasendiagramme
oder auch in Animationen darstellen. |