Phase 7:  Analog geht's mit den Algen ...

Die Entwicklung und Untersuchung eines analogen Algenmodells kann sowohl als selbständige Übertragung des Wasserpflanzenmodells durch die Schülerinnen und Schüler erfolgen (diesen - allerdings zeitaufwendigeren - Weg schlagen wir vor) als auch in arbeitsteiliger Gruppenarbeit zeitgleich mit der Entwicklung des Wasserpflanzenmodells.

Aufgabe 11:

Entwickle - analog zu dem Wasserpflanzenmodell - ein "Modell des Ressourcengesteueten Wachstums" für Algen und experimentiere damit!

Intendierte Lösung zu Aufgabe 11:

Algen verbrauchen - ebenso wie Wasserpflanzen - einerseits beim Wachstum Nährsalze, und andererseits reichern sie die verfügbare Nährsalzmenge beim Absterben wieder an. Dabei ist hypothetisch davon ausgegangen worden, daß -gemessen an der optimalen Zuwachsrate- jeweils 10% der Algen absterben. Diese hypothetische Schätzungen beruhen auf Erfahrungswerten zu der Differenz bei der Titerbestimmung durch Plattieren im Vergleich zum Auszählen: Beim Plattieren werden nur vitale Organismen erfaßt.

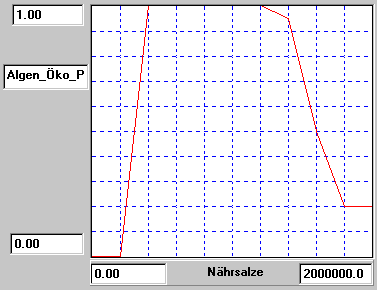
Algen sind i.d.R. an eutrophe (nährstoffreiche) Gewässer angepaßt, d.h. sie tolerieren hohe Nährsalzkonzentrationen, können aber niedrige Nährsalzkonzentrationen nicht verarbeiten. Letzteres kann durch eine Tabellenfunktion "Algen_Öko_Potenz" nachgebildet werden. In Abhängigkeit von der Aquariumgröße gibt es eine maximale Algen-Biomasse "Max_Algen", so daß das Algenwachstum ebenfalls als logistisches Wachstum beschrieben werden kann.

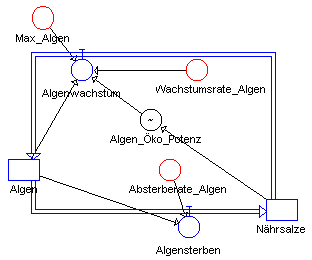
Das Modell selbst repräsentiert wieder einen Stoffkreislauf :

[algen5.dyn]

Zustandsgleichungen

Nährsalze.neu <-- Nährsalze.alt + dt*(Algensterben-Algenwachstum)
Startwert Nährsalze = 300000
Algen.neu <-- Algen.alt + dt*(Algenwachstum-Algensterben)
Startwert Algen = 10

Zustandsänderungen

Algenwachstum = Algen * Algen_Öko_Potenz
                              * Wachstumsrate_Algen*(1-Algen/Max_Algen)
Algensterben = Algen*Absterberate_Algen

Konstanten

Max_Algen = 10000000
Wachstumsrate_Algen = 1
Absterberate_Algen = 0,1

Zwischenwerte

Algen_Öko_Potenz = Tabelle(Nährsalze)
((0.00;0.00)(200000.00;0.00)(400000.00;1.00)(600000.00;1.00)
(800000.00;1.00)(1000000.00;1.00)(1200000.00;1.00)(1400000.00;0.95)
(1600000.00;0.50)(1800000.00;0.20)(2000000.00;0.20))

Simulation mit dem Modell aus Aufgabe 11:

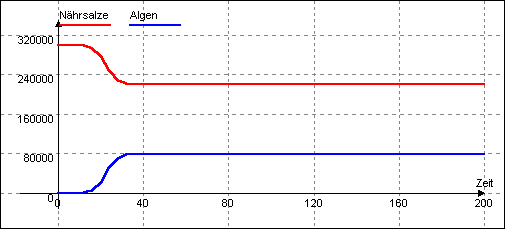
In dem Modell dieses geschlossenen Stoffkreislaufes ist so lange ein positives Nettowachstum (Zuwachs-Absterben) der Algenpopulation zu verzeichnen, bis die sich reduzierende Nährsalzkonzentration die Bruttowachstumsrate gleich der Absterberate werden läßt. Dann stellt sich ein Fließgleichgewicht ein. (Man beachte die optische Ähnlichkeit der Wachtsumskurve mit der des logistischen Wachstums.)

©   Helmut Kohorst   &  Philipp Portscheller   01.08.1996

[Weiter] [Zurück zum Inhaltsverzeichnis]