Phase 5: Auch Wasserpflanzen sterben ...

Aufgabe 7:

Pflanzen wachsen nicht nur, sondern es sterben ständig auch Pflanzen(teile) ab.
Erweitere das Modell in diesem Sinne, speichere es unter dem Namen "pflanz3.dyn", und lasse Dir vom Programm DYNASYS wieder ein Zeitdiagramm zur zukünftigen Entwicklung der Wasserpflanzenmenge zeigen!
Wie wirkt sich die Modell-Änderung auf das Wachstum der Wasserpflanzen aus?

Aufgabe 8:

Wasserpflanzen ernähren sich von im Wasser gelösten Nährsalzen. Andererseits werden die in abgestorbenen Pflanzenresten gebundenen Nährsalze wieder frei und stehen erneut zur Ernährung von Wasserpflanzen zur Verfügung.
Baue das Wasserpflanzen-Modell in diesem Sinne um, speichere das neue Modell unter dem Namen "pflanz4.dyn", und lasse Dir vom Programm DYNASYS wieder ein Zeitdiagramm zur zukünftigen Entwicklung der Wasserpflanzenmenge zeigen!
Wie wirkt sich diese Modell-Änderung auf das Wachstum der Wasserpflanzen aus?

Aufgabe 9:

Versuche, das mit dem Modell aus Aufgabe 8 erzielte unsinnige Simulationsergebnis zu erklären!
Kannst Du einen "Denkfehler" bei der Modellbildung erkennen?

Intendierte Lösung zu den Aufgaben 7-9:

zu Aufgabe 7:

[pflanz3.dyn]

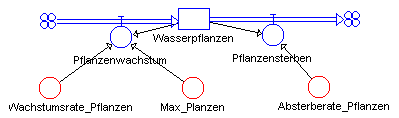
Zustandsgleichungen

Wasserpflanzen.neu <-- Wasserpflanzen.alt + dt*(Pflanzenwachstum-Pflanzensterben)
Startwert Wasserpflanzen = 1000

Zustandsänderungen

Pflanzenwachstum = Wasserpflanzen * Wachstumsrate_Pflanzen
                                  * (1-Wasserpflanzen/Max_Planzen)
Pflanzensterben = Wasserpflanzen*Absterberate_Pflanzen

Konstanten

Wachstumsrate_Pflanzen = 0,1
Max_Planzen = 10000000
Absterberate_Pflanzen = 0,01

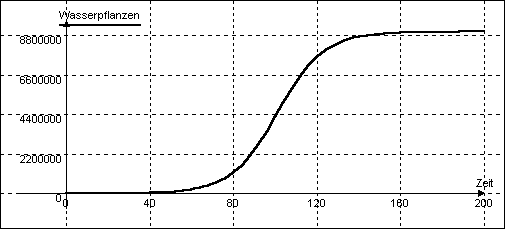
Die Simulation mit diesem erweiterten Modell zeigt gegenüber der vorigen lediglich eine etwas geringere Pflanzen-Maximalmenge, jedoch keine qualitativen Unterschiede:

zu Aufgabe 8:

Eine Lernschwierigkeit besteht darin zu verstehen, daß die Maßeinheit der beiden Zustandsgrößen identisch ist. Hinweise, daß man z.B. bei Angaben zur pflanzlichen Assimilatmenge ebenso wie bei Aussagen zu dem die Pflanze umgebenden Gasraum gleichermaßen auf Kohlendioxid als Einheit zurückgreifen kann, können hilfreich sein.

Das Modell selbst repräsentiert einen Stoffkreislauf. Wasserpflanzen nehmen Nährsalze auf, beim Absterben werden wieder über hier nicht dargestellte Prozesse Nährsalze frei. Dabei ist hypothetisch davon ausgegangen worden, daß -gemessen an der optimalen Zuwachsrate- jeweils 1% der Wasserpflanzen absterben.

[pflanz4.dyn]

Zustandsgleichungen

Wasserpflanzen.neu <-- Wasserpflanzen.alt + dt*(Pflanzenwachstum-Pflanzensterben)
Startwert Wasserpflanzen = 1000
Nährsalze.neu <-- Nährsalze.alt + dt*(Pflanzensterben-Pflanzenwachstum)
Startwert Nährsalze = 300000

Zustandsänderungen

Pflanzenwachstum = Wasserpflanzen * Wachstumsrate_Pflanzen
                                 * (1-Wasserpflanzen/Max_Planzen)
Pflanzensterben = Wasserpflanzen*Absterberate_Pflanzen

Konstanten

Wachstumsrate_Pflanzen = 0,1
Max_Planzen = 10000000
Absterberate_Pflanzen = 0,01

Die Simulation mit diesem Modell ergibt bzgl. der Nährsalzmenge ein (zumindest für "Unbedarfte") überraschendes Bild:

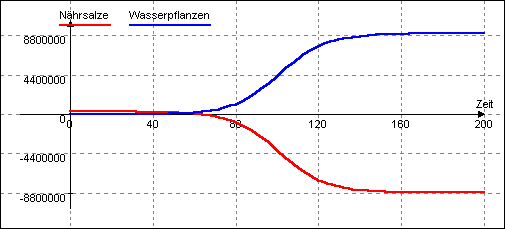
Der hier erstmals offensichtliche Modellfehler wird in der folgenden Aufgabe 9 thematisiert.

zu Aufgabe 9:

Natürlich muß in den bisherigen Modellen ein gravierender Modellfehler enthalten sein, denn der Nährsalzgehalt kann / darf natürlich nicht negativ werden.
Vielmehr müßte ein abnehmender Nährsalzgehalt zu einem verringerten Pflanzenwachstum führen.
In dem bisher betrachteten Modell haben wir jedoch das Pflanzenwachstum gar nicht in diesem Sinne vom jeweiligen Nährsalzgehalt abhängig gemacht.

Nicht beachtet wurde bisher:

Organismen benötigen zum Wachstum Ressourcen. Die vorhandenen Ressourcen regeln ihre Dichte, weil langfristig die natürlichen Bedingungen die der Knappheit und nicht die des Überflusses sind.

Ein wesentlicher Unterschied besteht zwischen heterotrophen und autotrophen Organismen. Letztere nehmen die notwendigen Substanzen getrennt voneinander auf. Der Minimumfaktor bestimmt dabei den Wachstumsprozeß.

Heterotrophe Organismen nehmen Nahrung paketweise auf. Der Nahrungsvorrat insgesamt begrenzt die Populationsdichte.

Empirisch besser zu untersuchen ist der Einfluß eines Faktors bei autotrophen Organismen:
Hält man experimentell alle Wachstumsfaktoren bis auf einen optimal und variiert diesen, erhält man die "ökologische Potenz" des Organismus bezogen auf diesen Faktor.

©   Helmut Kohorst   &  Philipp Portscheller   01.08.1996

[Weiter] [Zurück zum Inhaltsverzeichnis]