 Gesamtliste der
Modelle Gesamtliste der
Modelle
|
|
Modell
des linearen Wachstums
|
|
|
|
 |
|
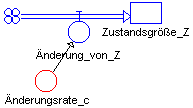
Wenn in einem dynamischen System nicht nur die
Änderungsrate c für die Zustandsgröße Z , sondern auch
die (absolute) Änderung von Z konstant ist, so bedeutet dies,
daß Z in gleichen Zeiteinheiten stets um den gleichen Wert wächst.
Dies ist etwa der Fall, wenn jemand in immer gleichen Zeitintervallen (z.B.
jeden Monat oder jedes Jahr jeweils am gleichen Datum) den gleichen Betrag
in seinen "Sparstrumpf" steckt und beobachtet, wie sein "Sparvermögen"
wächst. |
| Z
wächst in gleichen Zeiteinheiten stets um den gleichen
Wert |
|
Entsprechend heißt es in der Modellgleichung
für die Zustandsänderung in einem Zeitabschnitt: |
| Änderung_von_Z=Änderungsrate_c |
|
Mathematisch ausgedrückt handelt es sich bei
der Zustandsgröße Z also um eine Funktion der
Zeit t mit konstanter Steigung c , d.h. um eine Lineare
Funktion, deren Funktionsgleichung |
| Z(t) = c *
t + Zo |
|
bereits Siebtklässler leicht aus dem gegebenen Startwert
(= Hochachsen-Abschnitt) Zo und der Steigung c bestimmen
können. |
|
|
Drückt man den gleichen Sachverhalt in der
Sprache der Analysis aus, so hat man es hier zu tun mit der (elementaren)
Differentialgleichung: |
| (*)
Z'(t) = c |
|
Diese Differentialgleichung kann bereits mit wenigen
Analysis-Kenntnissen analytisch gelöst werden durch die oben bereits
elementar ermittelte Lineare Funktion, |
| Z(t) = c *
t + Zo |
|
wobei Zo wieder den Startwert (Anfangswert) der
Zustandsgröße Z bezeichnet. |
| "LINEARES
WACHSTUM" |
|
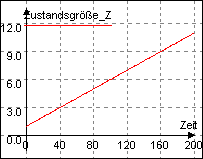
Die Zustandsgröße Z läßt sich also
mathematisch beschreiben durch eine lineare Funktion, und daher heißt
dieser Wachstumstyp "Lineares Wachstum". |
 |
|
DYNASYS und ebenso alle anderen Modellbildungs- und
Simulations-Programme lösen bei der Modellbildung entstehende
Differentialgleichungen wie die Gleichung (*) allerdings nicht
algebraisch-analytisch, sondern durchweg numerisch (vgl. die Rechenverfahren
nach "Euler-Cauchy" und
"Runge-Kutta"), denn für die meisten
Differentialgleichungen gibt es keine "geschlossenen" Lösungen. |