Gesamtliste der Modelle
 Das Euler-Cauchy-Verfahren für kontinuierliche Systeme
Die Aufgabe:

Numerische Lösung
einer Differentialgleichung
(eines Anfangswertproblems)

 Von einer Zustandsgröße Z seien bekannt:
  • der aktuelle Wert Z(to) zum Zeitpunkt to, d.h. anschaulich: ein Punkt A(to;Z(to)).
  • eine Differentialgleichung
    Z'(t) = f ( t ; Z(t) )      
    für die momentane Änderungsrate Z'(t) bzw. - anschaulich gesprochen - für die
    Steigung m=m(t)=Z'(t)  zu einem beliebigen Zeitpunkt t     .
Das Ziel:

Bestimmung von Prognosewerten

 Gesucht ist nun ein Prognosewert P(to+dt)
für den leider unbekannten tatsächlichen Wert Z(to+dt) nach einer gewissen Zeitspanne dt.
Die Idee des Euler-Cauchy-Verfahrens:
Lineare Fortsetzung von Z
mit der Tangentenfunktion P		 Aus den obigen Angaben ( Punkt A und Steigung m =m(to) im Punkt A ) läßt sich mit Hilfe des "Steigungsdreiecks" eine lineare Funktion P ermitteln, denn es ist (vgl. die folgende Skizze)
  

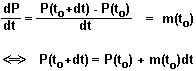Steigung als Differenzenquotient

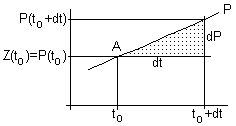 Euler-Cauchy-Verfahren Graphik 1
Diese lineare Funktion P läßt sich interpretieren als "Lineare Fortsetzung" der Funktion Z vom Zeitpunkt to bis zum Zeitpunkt to+dt.
Mathematisch ausgedrückt:
Die Prognose-Funktion P ist die Tangentenfunktion zur (differenzierbaren) Funktion Z im Zeitpunkt to.
Oft geht's ja sogar ... In all den Fällen, in denen der Graph von Z im betrachteten Zeitintervall dt nur wenig von einer Geraden abweicht, stellt der nach dem obigen Euler-Cauchy-Verfahren ermittelte Wert P(to+dt) einen brauchbaren Prognosewert für den vorherzusagenden Wert Z(to+dt) dar, denn in diesen Fällen gilt
 

Z(to+dt) ~ P(to+dt)

 Euler-Cauchy-Verfahren Graphik 2
Der zugehörige Punkt  B( to+dt ; P(to+dt ) wird als der gesuchte "nächste" Kurvenpunkt prognostiziert und dient als Startpunkt für den nächsten Euler-Cauchy-Iterationsschritt.
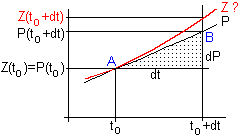
Wie sich die Funktion Z bzw. ihr Graph allerdings zwischen den Punkten A und B genau verhält, bleibt unbekannt und könnte nur durch eine Verfeinerung der Schrittweite näherungsweise ermittelt werden; dadurch würde sich jedoch auch der Prognosepunkt B ändern. 
... manchmal aber auch nicht ... Unglücklicherweise braucht die fragliche Funktion  Z  natürlich im betrachteten Zeitintervall  dt  nicht annähernd linear zu sein, wie z.B. die folgende Skizze zeigt:
... und dann heißt's:
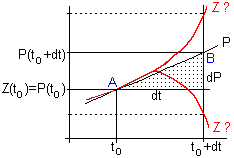"Dumm gelaufen!  Was nun ...?"		 Euler-Cauchy-Verfahren Graphik 3
Beispiel für die fortschreitende Fehlervergrößerung bei der
Schrittweite dt=0,25		 Das folgende konkrete Beispiel zeigt, wie schnell - selbst bei einer "gutmütigen" Funktion - das Euler-Cauchy-Verfahren durch den Verfahrensfehler zu im Grunde unbrauchbaren Prognosewerten führt bzw. führen kann.
Exakte (analytische) Berechnung
Das gegebene Anfangswertproblem
hat die Lösungsfunktion Z(t) = et - t , also ist der exakte Funktionswert
Z(1) = e - 1 = 1,71828...
Gegeben sei die Differentialgleichung
Z'(t) = Z(t) + t - 1 mit Anfangswert  Z(0) = 1.
Die hier zur Verdeutlichung gewählte Schrittweite dt=0,25 ist allerdings untypisch groß - üblich wäre etwa dt=0,1 mit spürbarem Genauigkeitsgewinn.
Numerische Lösung
nach Euler-Cauchy

Prognose nach Euler-Cauchy
m(0) = Z'(0) = Z(0)+0-1 = 1-1 = 0
Z(0,25) = Z(0)+m(0)dt = 1+0 = 1
m(0,25) = Z'(0,25) = 0,25
Z(0,5)=Z(0,25)+m(0,25)dt=1,0625
m(0,5) = Z'(0,5) = 0,5625
Z(0,75)=Z(0,5)+m(0,5)dt=1,203125
m(0,75) = Z'(0,75) = 0,953125
Z(1)=Z(0,75)+m(0,75)dt=1,4414...,
und damit weicht der "Euler-Cauchy-Prognosewert"
nach nur 4 Schritten bereits um
ca. 0,28 vom exakten Wert ab (gemessen an der tatsächlichen Zunahme beträgt die Wachstums- Fehlerquote also bereits ca. 39%).

Graphische Darstellung des
(einfachen) Euler-Cauchy-Verfahrens
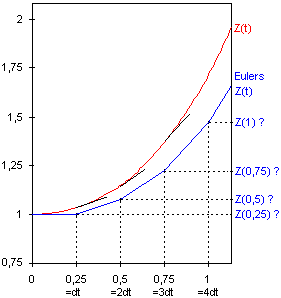mit eingetragener Lösungsfunktion Euler-Cauchy-Verfahren Graphik 4
Verfahrensfehler Man versucht, den beim Euler-Cauchy-Verfahren auftretenden Verfahrensfehler ggf. durch eine Verkleinerung der Schrittweite bzw. des Zeitintervalls dt zu vermindern, was jedoch ungünstigerweise gerade bei diskreten Systemen oft nicht (mehr) zulässig ist.
Wer's genauer wissen will ... Genauere Untersuchungen hinsichtlich der Auswirkungen unterschiedlicher dt-Wahlen beim (einfachen) Euler-Cauchy-Verfahren sind am Beispiel des exponentiellen Wachstums zusammengestellt auf der Seite
Diskretisierung eines kontinuierlichen Systems
und numerische Lösung ...
Rundungsfehler Eine solche Verminderung des Verfahrensfehlers  erkauft man allerdings i.a. damit, dass dann bei einer größeren Zahl von Rechenschritten (Iterationsschritten) bis zum Erreichen der vorgewählten "Prognose-Endzeit" größere Rundungsfehler auftreten können.
Fehlerüberlagerung

Wie man sich auch dreht und wendet, der .... bleibt hinten! (Volksweisheit)

 Man kann also Fehler prinzipiell nicht vermeiden, und es bleibt obendrein unklar, in welcher Weise Verfahrens- und Rechen- bzw. Rundungsfehler den Gesamtfehler vergrößernd oder verkleinernd beeinflussen. Es ist vielmehr durchaus möglich, daß sich die Fehler bis zu ersichtlich unsinnigen Rechenergebnissen verstärken. Dies gilt in besonderem Maße für periodische Abläufe, so daß hier leicht der Eindruck eines chaotischen Verhaltens entstehen kann, obwohl dieses in der Realität gar nicht vorliegt.
Fazit Oft bietet das Euler-Cauchy-Verfahren bei diskreten Systemen und vor allem bei hinreichend kurzen Prognosezeiträumen eine noch annehmbare Genauigkeit - bei diskreten Systemen hat man ja im Grunde auch gar keine Alternative.
Für kontinuierliche Systeme bzw. längere Prognosezeiträume reicht jedoch die selbst bei kleinem dt  mit dem Euler-Cauchy-Verfahren erzielbare Genauigkeit in aller Regel nicht aus.
Hier bedient man sich des deutlich aufwendigeren, aber auch genaueren Runge-Kutta-Verfahrens, das mit mehreren Stützstellen im Zeitintervall dt arbeitet und deren Einfluß auf den Prognosewert auch noch unterschiedlich gewichtet.
Vorsicht !
Hier müssen Sie selber nachdenken!		 Auswahlprobleme mit den Rechenverfahren
Unterrichtsprobleme mit den Rechenverfahren
Kopf der Seite © Goldkuhle, Kohorst, Portscheller 23.3.1997