 Gesamtliste der
Modelle Gesamtliste der
Modelle
|
|
Auswahlprobleme
mit den Rechenverfahren
|
|
|
|
| Problem
1: |
|
Bei den Erläuterungen zum
(einfachen) Euler-Cauchy-Verfahren und zum
Runge-Kutta-Verfahren (4. Ordnung)
wurde jeweils das gleiche Anfangswertproblem als Beispiel herangezogen: |
|
|
| Differentialgleichung |
Z'(t) = Z(t) + t - 1 |
| Anfangswert |
Z(0) = 1 |
| analytische Lösung |
Z(t) = et -1
Z(1) = e - 1 = 1,71828.. |
|
|
|
Dabei ergaben sich - mit jeweils etwa gleichem
Rechenaufwand - für Z(1) die folgenden numerischen
Lösungen:
| |
Euler-Cauchy |
Runge-Kutta |
| Schrittweite |
dt = 0,25 |
dt = 1 |
| Z(1) numerisch |
1,4414... |
1,70833... |
| Abweichung von der analytischen Lösung |
ca. 0,28 |
ca. 0,01 |
|
| Zur
Diskussion |
|
Welche "Lösung" für Z(1) ist
"besser", wenn
-
a) ein diskretes System mit
Schrittweite 0,25
-
b) ein kontinuierliches System
zugrunde gelegt wird ?
|
| Problem
2:
|
|
Ein Geldinstitut wirbt:
"Zur Geburt schenken wir Ihrem Kind ein Spar-Sonderkonto mit 5,- DM
Guthaben!"
( Jahreszinssatz 5 % , vierteljährliche Zinsgutschrift
)
Was ist dieses Geschenk eigentlich "wert", wenn man
das Spar-Sonderkonto viele Jahre lang unangetastet
läßt?
|
Ein
DYNASYS-Modell
ist schnell erstellt: |
|
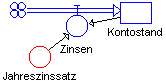
Startwert Kontostand = 5
Jahreszinssatz = 0,05
Zinsen = Jahreszinssatz * Kontostand
|
| Doch nun
die "Gretchenfrage" |
|
Welches Rechenverfahren mit welcher Schrittweite
soll bzw. muß man hier für eine Simulation - z.B. über
100 Jahre - wählen ? |
|
|
Unsicher probiert man etwa folgende vier Simulationen
mit recht unterschiedlichen Ergebnissen:
| |
Verfahren |
Schrittweite |
Betrag nach
100 Jahren |
| 1. |
Euler-Cauchy |
dt = 1 |
657,51 DM |
| 2. |
Euler-Cauchy |
dt = 0,25 |
719,42 DM |
| 3. |
Runge-Kutta |
dt = 1 |
742,07 DM |
| 4. |
Runge-Kutta |
dt = 0,25 |
742,07 DM |
|
| Zur
Diskussion
|
|
-
Warum liefern die 3. und 4. Simulation das gleiche Ergebnis?
-
Welche Simulation ist eigentlich "richtig"?
-
Warum gerade diese?
-
Und warum sind die anderen "falsch"?
|