Phase 4: Eine Korrektur des Wasserpflanzen-Modells

Aufgabe 5:

Warum wäre für ein echtes Aquarium ein unbegrenztes exponentielles Wachstum der Wasserpflanzenmenge unrealistisch?
Gibt es Faktoren, die das Wachstum der Wasserpflanzen auch dann begrenzen würden, wenn bezüglich ihrer Nährstoffversorgung stets optimale Bedingungen herrschen würden?
Wie könnte man eine solche Begrenzung des exponentiellen Wachstums mathematisch realisieren?

Aufgabe 6:

Verbessere mit Hilfe Deiner Lehrerin bzw. Deines Lehrers das Modell in diesem Sinne, speichere es unter dem Namen "pflanz2.dyn", und lasse Dir dann vom Programm DYNASYS die aufgrund des neuen Modells zu erwartende Entwicklung der Wasserpflanzenmenge zeigen!

Intendierte Lösung zu den Aufgaben 5 und 6:

zu Aufgabe 5:

Ein "echtes" Aquarium hat zweifellos nur eine beschränkte Größe, durch die natürlich auch die Menge der darin befindlichen Wasserpflanzen begrenzt wird, so daß das Wachstum sicher nicht unbegrenzt verlaufen kann, sondern auf irgendeine Weise gebremst wird.

Typisch für die Modellierung solcher gebremster Wachstumsvorgänge ist die Annahme, daß es eine von den jeweils vorhandenen Ressourcen (hier zunächst: der Aquarium-Größe) abhängige bestimmte feste Grenze "Z_extrem" für die Entwicklung der betrachteten Zustandsgröße Z (=Wasserpflanzenmenge) gibt.

Ist der Abstand zu diesem Grenzwert noch groß, so verläuft das Wachstum noch (annähernd) exponentiell. Je mehr sich aber der Wert der Zustandsgröße Z dem Grenzwert "Z_extrem" nähert, desto stärker wirken sich die begrenzenden Faktoren wachstumshemmend aus, bis schließlich, damit der Grenzwert nicht überschritten wird, Nullwachstum erreicht wird.

Wie man einen solchen Bremsvorgang im Modell nachbilden kann, zeigt der Dritte Mathematische Exkurs "Modell des Logistischen Wachstums".

zu Aufgabe 6:

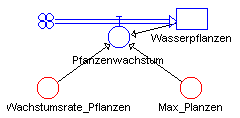
Nach der entsprechenden Änderung bzw. Ergänzung erhält das Modell folgende Gestalt:

DYNASYS-Modell "pflanz2.dyn"
[pflanz2.dyn]

Zustandsgleichungen

Wasserpflanzen.neu <-- Wasserpflanzen.alt + dt*(Pflanzenwachstum)
Startwert Wasserpflanzen = 1000

Zustandsänderungen

Pflanzenwachstum = Wasserpflanzen * Wachstumsrate_Pflanzen
* (1-Wasserpflanzen/Max_Planzen)

Konstanten

Wachstumsrate_Pflanzen = 0,1
Max_Planzen = 10000000

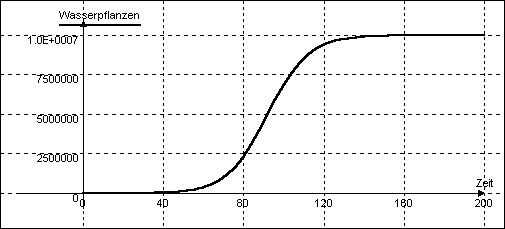
Nun ergibt sich für die Entwicklung der Wasserpflanzenmenge in dem Modellaquarium ein viel realistischeres Bild:

DYNASYS-Simulation "pflanz2.dyn"

[Weiter] [Zurück zum Inhaltsverzeichnis]