Dritter Mathematischer Exkurs: Modell des Logistischen Wachstums

Dritter Mathematischer Exkurs:

Modell des Logistischen Wachstums

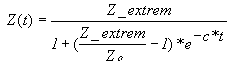
Besteht für das Wachstum einer Zustandsgröße Z eine feste obere Grenze "Z_extrem" , so muß das Wachstum derart gebremst werden, daß diese Grenze nicht überschritten werden kann.

Eine solche Entwicklung kann man mit Hilfe des zusätzlichen Korrekturfaktors

(1 - Z / Z_extrem)

in der zum exponentiellen Wachstum gehörigen Gleichung

(*) Änderung_von_Z = Änderungsrate_c * Z

(vgl. Erster Mathematischer Exkurs: "Modell des Exponentiellen Wachstums") nachbilden.

Dieser Korrekturfaktor ist bei großem Abstand zwischen dem Wert Z der Zustandsgröße und dem Grenzwert "Z_extrem" nahezu =1, ändert dann also fast nichts am exponentiellen Wachstum; bei sehr kleinem Abstand dieser Werte jedoch ist er nahezu =0 und läßt damit (fast) keine Änderungen der Zustandsgröße Z mehr zu.

Aus der zum exponentiellen Wachstum gehörigen Gleichung ergibt sich durch Einführung dieses Korrekturfaktors als neue Gleichung (**) für die Änderung in einem Zeitabschnitt:

(**) Änderung_von_Z = (1 - Z / Z_extrem) * Änderungsrate_c * Z

Mathematisch ausgedrückt ³⁾ ist der Korrekturfaktor eine streng monoton fallende Funktion mit Maximum 1 und Grenzwert 0, und die entstehende Gleichung ist die Differentialgleichung

Z'(t) = (1 - Z(t) / Z_extrem) * c * Z(t)

Diese Differentialgleichung wird gelöst ⁴⁾ durch eine Logistische Funktion

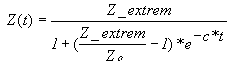
Logistische Lösungsfunktion

wobei Z_o den Startwert (Anfangswert) der Zustandsgröße Z bezeichnet.

Daher heißt dieser Wachstumstyp "LOGISTISCHES WACHSTUM"

Anmerkung 3):
Eine solche mathematische Ausdrucks- und Schreibweise ist natürlich für Schülerinnen und Schüler einer 8.Klasse noch nicht verständlich und sollte deswegen auch im Unterricht unterbleiben.

Anmerkung 4):
DYNASYS und ebenso alle anderen Modellbildungs- und Simulations-Programme lösen bei der Modellbildung entstehende Differentialgleichungen wie die Gleichung (**) allerdings nicht algebraisch-analytisch, sondern durchweg numerisch (vgl. den Zweiten Mathematischen Exkurs: "Mathematische Verfahren zur Ermittlung von Prognosewerten"), denn für die meisten Differentialgleichungen gibt es keine "geschlossenen" Lösungen.

[Zurück zum Inhaltsverzeichnis]