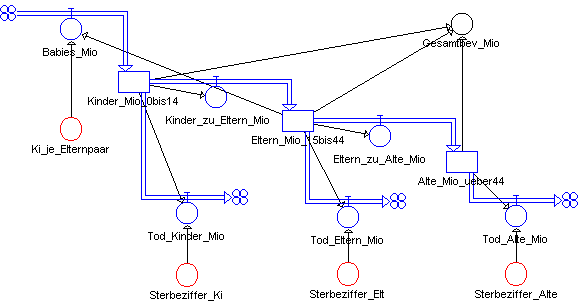
[china90b.dyn]
Die chinesische Bevölkerungspolitik wird oft als "1-Kind-Politik" bezeichnet. Damit ist gemeint, daß jedes Elternpaar im Laufe seines Lebens nur noch 1 Kind zeugen soll. Wie die Tabelle (M2) zeigt, betrug diese Zahl im Jahr 1990 noch durchschnittlich 2,42.
Auf welche Weise müßte man das bisherige Bevölkerungsmodell modifizieren, um darin die "durchschnittliche Kinderzahl je Elternpaar" berücksichtigen zu können?
Zeichne unter Verwendung der entsprechenden DYNASYS-Symbole eine geeignete Modellstruktur dafür auf !
Lade das Programm DYNASYS und öffne dort die Datei "china90b.dyn". Beschreibe das dargestellte Bevölkerungsmodell und vergleiche es mit Deinem Vorschlag!
Öffne in der Datei 'china90b.dyn' die Symbole mit einem Doppelklick, trage die jeweiligen Informationen in folgende Tabelle ein, und erkläre die mit * bezeichneten Berechnungsformeln !
Welche Vereinfachungen nimmt das Modell gegenüber einer realen (der chinesischen) Bevölkerung vor ?
| Kinder_Mio_0bis14 | Startwert = | ............................................................ | |
| Eltern_Mio_15bis44 | Startwert = | ............................................................ | |
| Alte_Mio_ueber44 | Startwert = | ............................................................ | |
| Ki_je_Elternpaar |
= |
............................................................ | |
| * | Babies_Mio |
= |
............................................................ |
| * | Kinder_zu_Eltern_Mio |
= |
............................................................ |
| * | Eltern_zu_Alte_Mio |
= |
............................................................ |
| Sterbeziffer_Ki |
= |
............................................................ | |
| * | Tod_Kinder_Mio |
= |
............................................................ |
| Sterbeziffer_Eltern |
= |
............................................................ | |
| * | Tod_Eltern_Mio |
= |
............................................................ |
| Sterbeziffer_Alte |
= |
............................................................ | |
| * | Tod_Alte_Mio |
= |
............................................................ |
| * | Gesamtbev_Mio |
= |
............................................................ |
Die im Modell 'china90b.dyn' benutzten Startwerte und Konstanten entstammen verschiedenen Statistiken zur Bevölkerung Chinas im Jahr 1990.
Berechne - per Hand bzw. mit einem Taschenrechner - anhand der Modelldaten und der von Dir notierten Formeln die Größe der Altersgruppen und der Gesamtbevölkerung Chinas nach einem Jahr !
Die Schülerinnen und Schüler haben nach Lösung der Aufgabe 8 bisher nur das Bild eines qualitativen Modells, dessen Struktur zunächst nochmals erläutert und mit dem der Datei "china90b.dyn" verglichen werden soll (Aufg. 9). Später wird dieses Modell "aufgeklappt" und erklärt (Aufg.10/11) sowie in den nächsten beiden Projektphasen für zielgerichtete Experimente genutzt (Aufg.12-15).
Zustandsgleichungen
Kinder_Mio_0bis14.neu <-- Kinder_Mio_0bis14.alt
+ dt*(Babies_Mio-Kinder_zu_Eltern_Mio-Tod_Kinder_Mio)
Startwert Kinder_Mio_0bis14 = 306,9
Eltern_Mio_15bis44.neu <-- Eltern_Mio_15bis44.alt
+ dt*(Kinder_zu_Eltern_Mio - Eltern_zu_Alte_Mio - Tod_Eltern_Mio)
Startwert Eltern_Mio_15bis44 = 589,2
Alte_Mio_ueber44.neu <-- Alte_Mio_ueber44.alt +
dt*(Eltern_zu_Alte_Mio-Tod_Alte_Mio)
Startwert Alte_Mio_ueber44 = 237,9
Zustandsänderungen
Babies_Mio = (Ki_je_Elternpaar/30) * Eltern_Mio_15bis44/2
denn nur die Hälfte der Eltern sind gebährfähige
Frauen, und deren Kinderzahl verteilt sich
auf die 30 Jahre Verweildauer in dieser Altersgruppe
Kinder_zu_Eltern_Mio = Kinder_Mio_0bis14 * (1/15)
denn in jedem Jahr wird 1/15 der Kinder 15 Jahre alt und
wechselt die Altersgruppe
Eltern_zu_Alte_Mio = Eltern_Mio_15bis44 * (1/30)
denn in jedem Jahr wird 1/30 der Eltern 45 Jahre alt und
wechselt die Altersgruppe
Tod_Kinder_Mio = Kinder_Mio_0bis14 * Sterbeziffer_Ki
Tod_Eltern_Mio = Eltern_Mio_15bis44 * Sterbeziffer_Elt
Tod_Alte_Mio = Alte_Mio_ueber44 * Sterbeziffer_Alte
Konstanten
Ki_je_Elternpaar = 2,42
Sterbeziffer_Ki = 1,3/1000
Sterbeziffer_Elt = 1/1000
Sterbeziffer_Alte = 25,7/1000
Zwischenwerte
Gesamtbev_Mio = Kinder_Mio_0bis14 + Eltern_Mio_15bis44 + Alte_Mio_ueber44
| Babies | (2,42 / 30 * 589,2 / 2) Mio |
23,764 Mio |
| Kinder_zu_Eltern | (306,9 / 15) Mio |
20,460 Mio |
| Tod_Kinder | (306,9 * 0,0013) Mio |
0,399 Mio |
| Kinder | (306,9 + 23,764 - 20,460- 0,399) Mio |
309,805 Mio |
| Eltern_zu_Alte | (589,2 / 30) Mio |
19,640 Mio |
| Tod_Eltern | (589,2 * 0,001) Mio |
0,589 Mio |
| Eltern | (589,2 + 20,460 - 19,640 - 0,589) Mio |
589,431 Mio |
| Tod_Alte | (237,9 * 0,0257) Mio |
6,114 Mio |
| Alte | (237,9 + 19,640 - 6,114) Mio |
251,426 Mio |
| Gesamtbevölkerung | (309,805 + 589,431 + 251,426) Mio |
1150,662 Mio |
© Helmut Kohorst 01.10.1996
[Weiter] [Zurück zum Inhaltsverzeichnis]