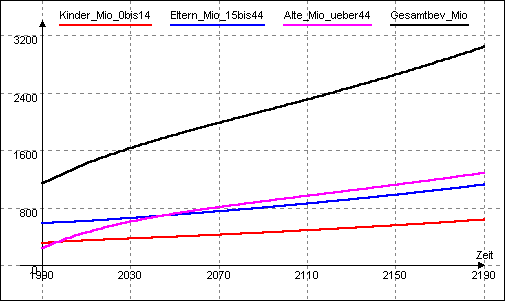
Erstelle mit Hilfe des Computers eine Prognose für die Bevölkerung Chinas für die Jahre 2000; 2025; 2050 und 2090 und beurteile sie! Lasse dazu vom Programm DYNASYS eine Tabelle und ein Zeitkurven-Diagramm erstellen!
Ermittle experimentell eine Kinderzahl je Elternpaar, für die bei unveränderten Sterberaten die Gesamtbevölkerung Chinas konstant bliebe bzw. nach einiger Zeit (wieviele Jahre?) würde !
Welche Bevölkerungsgröße und welche Altersgliederung lägen
bei der dann "stationären" Bevölkerung vor?
(Demographen nennen eine Bevölkerung "stationär", wenn sowohl die
Größe dieser Bevölkerung als auch ihre Altersgliederung
stagniert.)
Welche Bevölkerungsentwicklungen ergäben sich - wieder bei
unveränderten Sterberaten - bei einer kleineren (größeren)
Kinderzahl je Elternpaar?
Solche Untersuchungen, bei denen man nur einen Parameter variiert und die
übrigen unverändert läßt, nennt man auch
"ceteris-paribus-Analysen".
Welcher systematische Modellfehler wird in allen Simulationen der Aufgabe 12 deutlich?
Entwickle einen Vorschlag zur Behebung dieses Fehlers und speichere das (ggf. mit Lehrerhilfe) entsprechend korrigierte Modell unter dem Namen "china90c.dyn".
Wichtig ist bei Aufgabe 13 und später auch bei Aufgabe 15 (siehe Projektphase 7) das Experimentieren:
Einerseits sind die Aufgaben nur dadurch sinnvoll zu bearbeiten, und andererseits haben Schülerinnen und Schüler davor nach unseren Erfahrungen eine recht große Scheu, die im Verlauf dieser Phase überwunden werden muß!
Das Zeitdiagramm zeigt deutlich das sehr schnelle Wachstum der Bevölkerung Chinas bei 2,42 Kindern je Elternpaar. Dieses betrifft alle drei Altersgruppen, insbesondere aber (und vermutlich unerwartet) die Gruppe der Alten. Wäre diese Entwicklung realistisch, so bedeutete dies neben den bereits angesprochenen Problemen auch noch solche bzgl. der Altersversorgung.

Eine stationäre Bevölkerung ergäbe sich bei 2,1 Kindern je Elternpaar nach ca. 170 Jahren. Während die Altersgruppen der Kinder- und Eltern sich von vornherein nicht in ihrer Größe verändern würden, wüchse bis dahin die Gruppe der Alten deutlich an und wäre bereits nach ca. 100 Jahren die stärkste Gruppe, bis sie schließlich ca. 45% der Bevölkerung ausmachte.
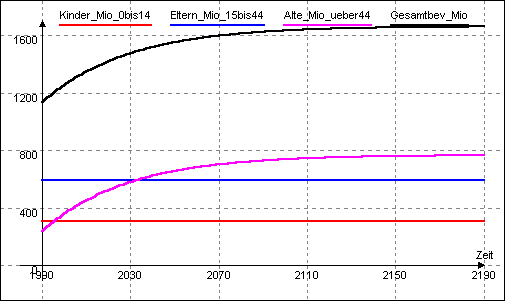
Bei einer größeren Kinderzahl je Elternpaar als 2,1 ergäbe sich wieder das Bild einer ständig wachsenden Bevölkerung, während bei einer kleineren als 2,1 die Bevölkerung nach einiger Zeit ein gewisses Maximum erreichen, dann wieder abnehmen und schließlich aussterben würde. Auch hier wäre jeweils v.a. die Entwicklung der Gruppe der Alten ausschlaggebend.
Bei 1,5 Kindern je Elternpaar ab 1990 ergäbe sich beispielsweise:
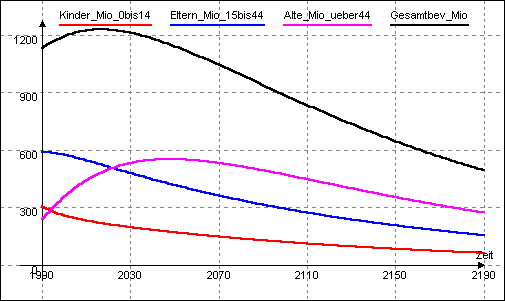
Würde die von China zur Zeit angestrebte Kinderzahl von 1,0 - beginnend 1990 - langfristig Bestand haben, so ergäbe sich das Bild einer deutlich schneller aussterbenden Bevölkerung, was wohl kaum in der Absicht der chinesischen Politiker liegen dürfte:
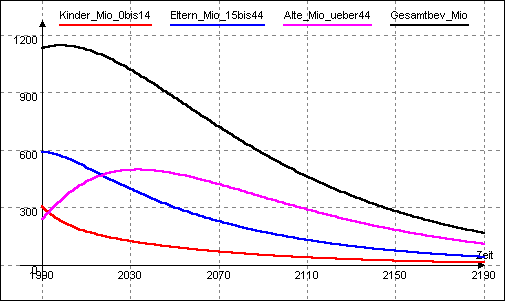
Da offenbar in jedem Falle nach einiger Zeit die Gruppe der Alten den größten Bevölkerungsanteil stellen würde, scheint es sich hier um einen systematischen Fehler des benutzten Bevölkerungsmodells zu handeln.Die Ursache ist wohl darin zu suchen, daß einerseits die Sterberate der "Alten" konstant gesetzt wurde, andererseits aber diese Gruppe immer weiter zunimmt und die dann zu niedrig angesetzte Sterberate zu einer zu langen (praktisch unbegrenzeten) Verweildauer in der Gruppe der "Alten" führt.
Eine mögliche Korrektur des Modells besteht z.B. in der Berücksichtigung der derzeitigen Lebenserwartung eines Chinesen bei seiner Geburt. Diese beträgt (laut Fischer Weltalmanach 1992) im Jahr 1990 ca. 70 Jahre, so daß von einer maximalen Verweildauer von 25 Jahren in der Gruppe der "Alten" ausgegangen werden kann.
Wenn man also - gleichstarke Jahrgänge auch in der Gruppe der "Alten" voraussetzend - davon ausgeht, daß jährlich mindestens 1/25 der "Alten" stirbt, so müßte dementsprechend im Modell lediglich die Vorschrift für die Zustandsänderung "Tod_Alte_Mio" geändert werden in:
Tod_Alte_Mio = MAX (Alte_Mio_ueber44 * Sterbeziffer_Alte ; Alte_Mio_ueber44 / 25)
Als Beispiel für die Auswirkung dieser Änderung hier noch einmal das Zeitkurven-Diagramm bei 2,42 Kindern je Elternpaar, jetzt allerdings mit dem korrigierten Modell "china90c.dyn":
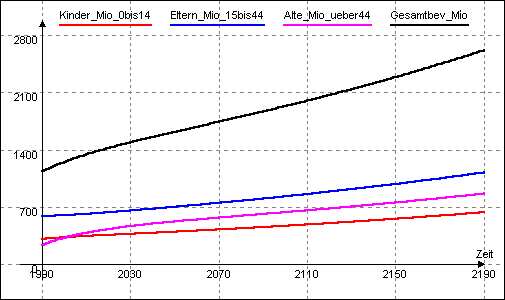
Das Diagramm zeigt deutlich das nun sehr viel geringere Wachstum der Altengeneration und damit ebenfalls der Gesamtbevölkerung. Auch die damit verbundene Altersgliederung entspricht nun eher den Erwartungen:
Wie entsprechende Berechnungen auf der Grundlage der zu dieser Simulation gehörigen Tabelle ergeben, würde im dargestellten Zeitraum
Dies entspräche einer durchaus im denkbaren Bereich liegenden Bevölkerungspyramiden-Entwicklung von einer ausgeprägten Glockenform zu einer beinahe rechteckigen Form als Übergang auf dem Weg zur Urnenform, wie sie heute von Demographen z.B. für die BR Deutschland etwa im Jahr 2030 prognostiziert wird.
© Helmut Kohorst 01.10.1996
[Weiter] [Zurück zum Inhaltsverzeichnis]