Gesamtliste der Modelle
 Das Euler-Cauchy-Verfahren
für diskrete Systeme
Die Aufgabe:
Lösung eines diskreten Anfangswertproblems

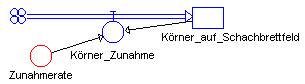
Von einer Zustandsgröße Z seien bekannt:
  • der aktuelle Wert Z(to) zum Zeitpunkt to, d.h. anschaulich: ein Punkt A(to;Z(to)).
  • die während der Zeitspanne dt konstante Änderungsrate m(to) von  Z(t)  bzw. - anschaulich gesprochen - die während der Zeitspanne  dt  konstante Steigung  m(to). 

Gesucht ist nun der jeweils nächste Wert  Z(to+dt) der Zustandsgröße  Z  nach einer gewissen Zeitspanne dt.
 
Die Idee des Euler-Cauchy-Verfahrens: Im Falle eines diskreten Systems ist die Änderungsrate bzw. Steigung  m  innerhalb einer Zeitspanne  dt  konstant. Daher ist der Graph der betrachteten Zustandsgröße  Z  ein Streckenzug, dessen Verlauf bis auf rechner- bzw. speicherbedingte Rundungsfehler exakt ermittelt werden kann.
 
Berechnung des jeweils nächsten Wertes  Z(to+dt)  mit Hilfe
einer Differenzengleichung		 Zur Berechnung von  Z(to+dt)  lässt sich nämlich aus den obigen Angaben
(Punkt A und Steigung m(to) im Punkt A)
mit Hilfe des "Steigungsdreiecks" eine Differenzengleichung aufstellen, denn es ist (vgl. die folgende Skizze)



Daraus ergibt sich die Differenzengleichung
  
dZ  =  Z(to+dt)  -  Z(to)  =  m(to)*dt
 
und daraus schließlich
 
Z(to+dt)  =  Z(to) + m(to)*dt  

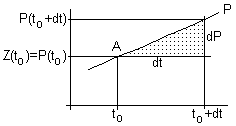[ Dynasys schreibt eine solche Gleichung
     in der Form  Z.neu  <--  Z.alt + dt * m ]
 
Der so bis auf eventuelle Rundungsfehler exakt errechnete nächste Punkt  B( to+dt ; Z(to+dt) ) des Streckenzuges  Z(t)  dient als Startpunkt für den nächsten Euler-Cauchy- Iterationsschritt usw.
 
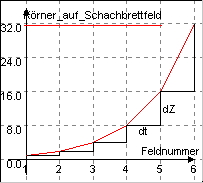
Beispiel:
Sullas Weizenkörner :

In einer persischen Sage erbittet der Gewinner eines Schachspiels vom unterlegenen König auf das erste Feld ein Weizenkorn, auf das zweite Feld zwei Weizenkörner, auf das dritte Feld vier Weizenkörner usw....
Der König überlegt nicht lange und geht auf diesen bescheidenen Wunsch hocherfreut ein.
Hättest Du genauso gehandelt?

Überlege dazu, wieviel Weizenkörner du als König auf das 4.,5.,...,64. (letzte) Feld des Schachbrettes legen und wieviel Weizenkörner Du insgesamt für Deine Niederlage "bezahlen" müßtest.

 

Anzahl Körner auf einem Feld

 

 

Zustandsgleichung
Körner_auf_Schachbrettfeld.neu <--
   Körner_auf_Schachbrettfeld.alt+dt*(Körner_Zunahme)
Startwert
Körner_auf_Schachbrettfeld = 1
Zustandsänderungen
Körner_Zunahme =
   Körner_auf_Schachbrettfeld*Zunahmerate
Konstanten
Zunahmerate = 1    {also 100% bzw. Verdoppelung}

 

In diesem Beispiel ist  dt=1.
Das Euler-Cauchy-Verfahren rechnet dann so:
Wenn auf dem to = 4. Schachbrettfeld bereits
Z(to) = 8  Körner liegen, dann müssen auf das
to+dt = 5. Schachbrettfeld zusätzlich noch 
Körner_Zunahme*dt = m(to)*dt = dZ = Körner_auf_Schachbrettfeld*Zunahmerate*dt = 8*1 *1= 8  Körner mehr gelegt werden, so dass dorthin insgesamt  Z(to+dt) = Z(to)+m(to)*dt =
Z(to)+dZ = 8+8=16  Körner zu legen sind.

Wenn auf dem to = 5. Schachbrettfeld bereits
Z(to) = 16 Körner liegen, dann müssen ..... usw.

Die Rechnung ist in diesem Beispiel solange exakt, bis die Körnerzahlen für eine genaue Darstellung zu groß werden:
Für das 34.Feld errechnen sich noch exakt 8.589.934.592 Körner, während es ab dem 35.Feld ( ca. 1,717987 E+0010 = 17.179.870.000 Körner) zu rechner- bzw. speicherbedingten Rundungen kommt (816 Körner zuviel). Dieser Rundungsfehler vergrößert sich zwar von Feld zu Feld weiter, im Verhältnis zu der jeweiligen Körnerzahl bleibt er aber lange ziemlich klein.
 
Fazit Im Grunde rechnet das Euler-Cauchy-Verfahren bei diskreten Systemen exakt und bietet daher bei hinreichend kurzen Prognosezeiträumen auch im Falle eventueller (rechner- bzw. speicherbedingter) Rundungsfehler eine gute Genauigkeit, da sich dann diese Fehler in der Regel nicht wesentlich "aufschaukeln" können.

Bei diskreten Systemen hat man auch gar keine Alternative, weil die Zeitspanne  dt  von der Problemstellung her festliegt.

Für kontinuierliche Systeme jedoch reicht die selbst bei Diskretisierungen mit kleinem dt  mit dem Euler-Cauchy-Verfahren erzielbare Genauigkeit in aller Regel nicht aus.
Hier bedient man sich des deutlich aufwändigeren, aber auch genaueren Runge-Kutta-Verfahrens, das mit mehreren Stützstellen im Zeitintervall dt arbeitet und deren Einfluss auf den Prognosewert auch noch unterschiedlich gewichtet.

Kopf der Seite

© Goldkuhle, Kohorst, Portscheller  06.04.2000