Learn:line NRW - Arbeitsbereich Modellbidlung und Simulation

Modelle

Diskretisierungseffekte beim Euler-Cauchy-Verfahren und beim Runge-Kutta-Verfahren am Beispiel des Exponentiellen Wachstums; Fehlerbetrachtungen

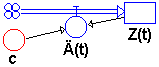
Von einer Zustandsgröße Z sei bekannt, dass sie - beginnend mit dem Startwert Z(0)=1 - kontinuierlich exponentiell wächst.
Die zugehörige Änderungsgleichung sei also m(t)=c*Z(t).

(Üblich ist statt m(t) die Bezeichnung Z'(t) , aber im Interesse von der Analysis unkundigen Schülerinnen und Schülern soll hier nicht von der Differentialgleichung Z'(t)=c*Z(t) gesprochen werden.)

Die (Schülerinnen und Schülern allerdings in der Regel unbekannte) analytische bzw. stetige Lösung dieses Problems lautet Z(t)=e^ct.

Diskretisierung als Vorbereitung einer numerischen Lösung Um für dieses Problem zu einer numerischen Lösung zu kommen, wird zunächst eine Diskretisierung in einzelne Zeitschritte dt>0 vorgenommen, also die Beschränkung auf diskrete Zeitpunkte t = ndt (beim einfachen Euler-Cauchy-Verfahren) bzw. t = ⁿ/₂dt (beim Runge-Kutta-Verfahren 4. Ordnung), wobei jeweils ID(n)=IN_oist.

Zur Anwendung des (einfachen) Euler-Cauchy-Verfahrens

Zeit	Zustandsgröße	Änderung
0dt	Z(0)=1	m(0) = c*Z(0)
1dt	Z(dt) = Z(0)+m(0)dt = 1+cdt	m(dt) = c*Z(dt) = c(1+cdt)
2dt	Z(2dt) = Z(dt)+m(dt)dt = (1+cdt)²	m(2dt) = c*Z(2dt) = c(1+cdt)²
....	....	....
ndt	Z(ndt) = (Z(dt))ⁿ = (1+cdt)ⁿ

Würde man in der Gleichung Z(ndt)=(1+cdt)ⁿ speziell die Schrittweite dt=1 benutzen, so erhielte man daraus die bekannte

Zinseszinsformel
bei jährlicher Verzinsung Z(n) = (1+c)ⁿ

Andererseits ergibt sich bei der

Rück-Substitution dt = ^t/_n : Z(t) = (1+^ct/_n)ⁿ --> e^ct für n --> unendlich

Fehlerbetrachtung Bei Z(dt) =1+cdt handelt es sich um die ersten beiden Summanden der zugehörigen
Taylor-Reihe e^cdt = .

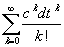Allgemein sagt man, der Fehler des Euler-Cauchy-Verfahrens sei von der Ordnung (dt)² .

Daraus wird deutlich, daß der
Fehler e^cdt - Z(dt) =
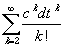
von der Ordnung (dt)² und mithin recht groß ist.

Verfahrens- und Rundungsfehler Dieser Verfahrensfehler wird zwar umso kleiner, je kleiner die Schrittweite dt gewählt wird, andererseits führt aber die Verkleinerung von dt zu einem höheren Rechenaufwand, und damit nimmt die Gefahr von spürbaren Rundungsfehlern erheblich zu, denn Computer rechnen bekanntlich nur mit einer endlichen Stellenzahl.
Insgesamt ist festzustellen, dass sich der Gesamtfehler beim Euler-Cauchy-Verfahren bei jeder festen Schrittweite dt mit zunehmender Schrittanzahl n sehr schnell spürbar vergrößern kann.

Wegen der Größenordnung des Fehlers und der damit einhergehenden schnellen Fehlervergrößerung wendet man bei kontinuierlichen Systemen nicht das Euler-Cauchy-Verfahren, sondern das Runge-Kutta-Verfahren (in der Regel 4.Odnung) an:

Zur Anwendung des Runge-Kutta-Verfahrens (4. Ordnung)

Zeit	Zustandsgröße	Änderung
0dt	Z(0)=1	Hilfsrechnung:
1dt		Hilfsrechnung wie oben liefert:
2dt		Hilfsrechnung wie oben liefert:
....	....	....
ndt

Bei der

Rück-Substitution dt = ^t/_n in der Gleichung
Z(ndt) =
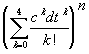
ergibt sich für n --> unendlich wieder
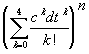Z(t) =--> e^ct ,
wobei die Konvergenz jedoch wesentlich schneller erfolgt als beim (einfachen) Euler-Cauchy-Verfahren.

Fehlerbetrachtung Bei Z(dt) =
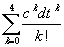
handelt es sich um die ersten fünf Summanden der zugehörigen
Taylor-Reihe e^cdt = .

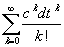Allgemein sagt man, der Fehler des Runge-Kutta-Verfahrens sei von der Ordnung (dt)⁵ . Daraus wird deutlich, dass der
Fehler e^cdt - Z(dt) =
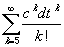
von der Ordnung (dt)⁵ und damit deutlich kleiner als der beim Euler-Cauchy-Verfahren ist.

Verfahrens- und Rundungsfehler Geringe Verkleinerungen der Schrittweite dt beeinflussen diesen Verfahrensfehler zwar verhältnismäßig wenig, vergrößern jedoch den Rechenaufwand erheblich, so dass es zu größeren Rundungsfehlern kommen kann, denn Computer rechnen bekanntlich nur mit einer endlichen Stellenzahl.

Experimente zu unterschiedlichen dt-Wahlen mit einer Tabellenkalkulation Wer die Auswirkungen unterschiedlicher dt-Wahlen und die Fehlervergrößerung bei zunehmender Schrittanzahl n am Beispiel des exponentiellen Wachstums experimentell genauer analysieren will, kann sich hier eine MS-WinWorks3-Tabelle "numerik.wks" als ZIP-File "numerik.zip" (33,2 K) herunterladen, die neben dem Runge-Kutta-Verfahren und dem einfachen Euler-Cauchy-Verfahren auch zwei Verbesserungen des Euler-Cauchy-Verfahrens zur Untersuchung anbietet.

und der Gesamtfehler?

Beide Fehlerarten entwickeln sich in Abhängigkeit von der Schrittweite dt gegensätzlich:
Wird die Schrittweite dt verringert, so verkleinert sich zwar der Diskretisierungsfehler, andererseits nimmt aber der numerische Fehler in der Regel zu. Wird dagegen die Schrittweite dt vergrößert, so verringert sich aufgrund der geringeren Anzahl der durchzuführenden Rechenschritte in der Regel der numerische Fehler, während andererseits der Diskretisierungsfehler wächst.

Offen blieb bei den bisherigen Fehlerbetrachtungen, wie sich Verfahrensfehler (= Diskretisierungsfehler) und Rundungsfehler (= numerische Fehler) nun auf den jeweiligen Gesamtfehler auswirken.

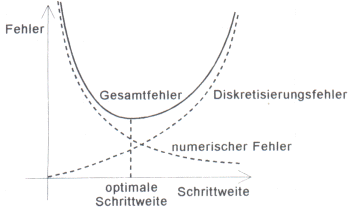
Gesamtfehler

Zumindest theoretisch gibt es jeweils für eine bestimmte Differentialgleichung zusammen mit einem bestimmten Näherungsverfahren eine optimale Schrittweite dt.
Es gelingt allerdings leider nur selten, diese optimale Schrittweite konkret anzugeben.

Festzustellen ist jedenfalls, dass sich der Gesamtfehler bei fester Schrittweite dt mit zunehmender Schrittanzahl n auch beim Runge-Kutta-Verfahren 4.Ordnung mehr oder weniger spürbar vergrößern kann.

Faustregeln

Bei diskreten Systemen ist die Schrittweite dt vom System her vorgegeben - hier bleibt einem keine Wahl, sondern man ist auf das Euler-Cauchy-Verfahren angewiesen, das in diesem Falle glücklicherweise bis auf Rundungsfehler exakt rechnet.

Bei kontinuierlichen Systemen kann das Euler-Cauchy-Verfahren wegen der schnellen Fehlervergrößerung nur in besonderen Fällen und allenfalls bei sehr kurzen Prognosezeiträume noch einigermaßen vertretbar sein.

Hier wird man jedoch wegen der erheblich größeren Genauigkeit in aller Regel zum Runge-Kutta-Verfahren greifen. Zumindest bei "gutartigen" Funktionen (i.e. keine "Schwingungen") bleibt dann der Gesamtfehler normalerweise in vertretbaren Grenzen, während es bei "bösartigen" Funktionen (i.e."Schwingungen") und gewissen dt-Einstellungen leicht auch zu "chaotischen Verläufen" kommen kann (vgl. z.B. die Räuber-Beute-Systeme in diesem Arbeitsbereich).

Vorsicht !
Hier müssen Sie selber nachdenken! Auswahlprobleme mit den Rechenverfahren
Unterrichtsprobleme mit den Rechenverfahren

Kopf der Seite