zu
den Aufgabensequenzen |
|
Zur
Entstehung und Bedeutung von
Räuber-Beute-Modellen |
|
|
|
Nordamerika
im 17. - 19.Jhdt.: |
|
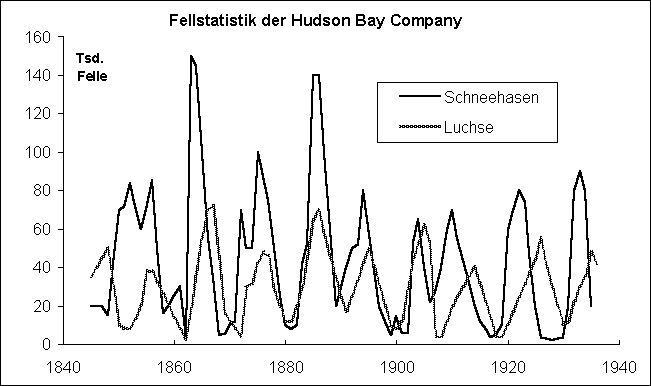
Im Raum
um die Hudson Bay betreibt die Hudson's Bay Company einen einträglichen
Handel mit Fellen u.a. von Luchsen und Schneehasen. Doch wie die akribischen
Aufzeichnungen der Company zeigen, schwanken die Erträge nicht
unerheblich:
|
 |
| |
| Periodische
Schwankungen in Populationsbeständen ... |
|
Erstaunlich
ist an diesen Aufzeichnungen, insbesondere wenn man von den angelieferten
Fellen auf die Populationsgrößen zurückschließt, vor
allem die erkennbare Regelmäßigkeit der charakteristisch
zeitverschobenen Schwankungen mit einer Periode von ca. 7-10 Jahren.
Ähnliche periodische Schwankungen können auch bei Fischbeständen
in der Adria nachgewiesen werden, wobei die Maxima der "Räuberpopulation"
stets mit einer gewissen Zeitverzögerung den Maxima der "Beutepopulation"
nachfolgen.
Diese Phänomene erwecken das Interesse sowohl des italienischen
Mathematikers Vito Volterra als auch des amerikanischen Biophysikers Alfred
Lotka: Sie wollen diesen Regelhaftigkeiten auf die Spur kommen.
|
| |
|
|
| ...
führen zu einem mathematischen Modell zur Beschreibung von
Räuber-Beute-Systemen |
|
Auf
der Suche nach Gründen für die gegeneinander verschobenen
Periodizitäten schließen sie besondere Verhaltensweisen
von Einzeltieren ebenso aus wie in der sozialen Organisation der Gattungen
liegende Ursachen.
Da Luchse hauptsächlich von Schneehasen leben und letztere in ihrem
kanadischen Lebensraum kaum andere Feinde haben, hegt Lotka den Verdacht,
die Ursache läge in spezifischen Räuber-Beute-Beziehungen der jeweils
beteiligten Tier-Populationen.
Ähnliche Überlegungen stellt auch Volterra bzgl. der adriatischen
Fischbestände an.
Schließlich veröffentlichen beide unabhängig voneinander
-
Volterra 1925 und
Lotka 1926 - ein mathematisches Modell zur Beschreibung der
Dynamik von Räuber-Beute-Systemen, das von
Hartmut Bossel 1985 in seinem Buch "Umweltdynamik" in
abgewandelter Form erneut veröffentlicht wird. |
| |
|
|
Zur
Bedeutung von Räuber-Beute-Modellen
aus heutiger Sicht |
|
--------- folgt vielleicht
demnächst -----------
|
| |
|
|
|
|
Literatur
: |
| Bossel,
H. |
|
Umweltdynamik
- 30 Programme für kybernetische Umwelterfahrungen auf jedem Basic-Rechner,
te-wi, München 1985 (nicht mehr im Handel) |
| Bossel,
H. |
|
Modellbildung
und Simulation, 2.Aufl., Vieweg-Verlag Braunschweig 1994 |
| Lotka,
A.J. |
|
Elements
of physical biology, Williams & Wilkins Co., Baltimore 1925
|
| Lotka,
A.J. |
|
Elements
of mathematical biology, Dover, New York 1956 |
| Volterra,
V. |
|
Variazioni
e fluttuazioni del numero d'individui in specie animali conviventi. Mem.
R. Accad. Naz. dei Lincei. Ser. VI, vol. 2., 1926 |
| Volterra,
V. |
|
Leçon
sur la theorie mathematique de la lutte pour la vie, Gauthier-Villars,
Paris 1931 |
| |
|
|
|
|
 ergänzende Links : |
| Lotka-Volterra
mit EXCEL |
|
http://www.ecotronics.ch/ecotron/excLotka.htm
mit  einer
Excel-Tabelle
(Dr.Silvia Rothen, rothen electronics, Bern, Schweiz,
1997-99) |
| Volterrasche
Gesetze und biologisches Gleichgewicht |
|
http://www.egbeck.de/skripten/bs11-27.htm
(EGBeck, berufl.Gymnasium Baden-Württemberg 1997) |
| Populationsökologie |
|
http://www.ento.vt.edu/~sharov/popechome/
(Alexei Sharov 1996) |
| Lotka-Volterra-Modell |
|
http://www.gypsymoth.ento.vt.edu/~sharov/PopEcol/lec10/lotka.html
mit einer
Excel-Tabelle (Alexei Sharov 1996) |
| Räuber-Beute-Simulation |
|
http://www.teorekol.lu.se/simulation_server/
(Online-Simulationen, Lund University) |
| Räuber-Beute-Simulation |
|
http://www.primenet.com/~lascaux/predprey.html |
| Lottka-Volterra
mit STELLA |
|
http://www.stolaf.edu/people/mckelvey/envision.dir/lotka-volt.html |
| Räuber-Beute-System
bei begrenzter Weidehaltung mit DYNASYS |
|
http://www.modsim.de
(W.Hupfeld) |
| Unterschiedliche
Zugangsweisen zu Naturphänomenen am Beispiel des
Lottka-Volterra-Modells |
|
mit der WayBack-Machine gerettet
ehemals:
http://www.diff.uni-tuebingen.de/person/wedekind/sim/schecker3.html
(H.Schecker, DIFF 1997) |
interner Link
