Gesamtliste der
Modelle
zurück |
|
Unterrichtliche
Anregungen |
|
|
|
Didaktischer Ort des
Modells |
|
Die Schülerinnen und Schüler sollten das
Grundmodell der Beziehung von Räuber und Beute
kennen, um so im Modell die Folgen des Zeitverzuges einschätzen
zu können. |
Instabiliät |
|
Das Grundproblem dieses Modellansatzes ist es, dass
das Modell in seinem Verhalten keine Tendenz zur Stabilität zeigt: Vielmehr
schaukeln sich die Populationsgrößen auf und schwanken zwischen
zunehmend höheren und zunehmend kleineren Werten mit Fortschreiten der
Simulationsdauer. |
Räuber, Beute und
Ressourcen |
|
Wenn man annimmt, dass sich auch ohne einen Räuber
eine Beute nicht beliebig vermehren kann, weil ihr Lebensraum per se limitiert
ist und diese Limitierung -hier als logistisches Wachstum
der Beute - in das Modell mit aufnimmt, was passiert dann
eigentlicht?
|
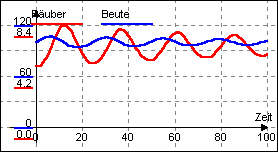
Die nebenstehende Graphik zeigt den Simulationslauf des erweiterten Räuber-
und Beutemodells, allerdings ist die Zahl der Beutetiere auf 300 begrenzt
worden:
(Beutegeburt=Beute*0,1*(1-Beute/300) |
|
 |
|
|
|