.

Der Artikel aus   mathematik lehren  ,  Heft 97 / 1999

Wozu Hefe nicht alles gut ist ...

Vom exponentiellen zum logistischen Wachstum

von

Helmut Kohorst und Philipp Portscheller

Hefe ist Schülerinnen und Schülern in der Regel wohlbekannt, dient der Hefepilz doch als wichtige Substanz nicht nur beim Backen, sondern auch bei der Produktion von Alkohol. Der Stoffwechsel dieses Organismus kann in der Oberstufenbiologie experimentell erforscht werden, im Rahmen eines Genetikkurses kann die Anzucht einer Hefekultur exemplarisch für die Kultur von Mikroorganismen überhaupt stehen.

Auf diesem Hintergrund könnte die Beschäftigung mit Hefe etwa im Rahmen eines fächerverbindenden Projekts im mathematisch-naturwissenschaftlichen Unterricht durchaus einen prominenten Stellenwert haben.

Der vorliegende Artikel soll zeigen, in welcher Weise sich der Mathematik-Unterricht ab Jahrgangstufe 10 im Rahmen der fortgeschrittenen Untersuchnung von nichtlinearen Wachstumsprozessen an einem solchen Vorhaben beteiligen könnte.

Die Behandlung von nichtlinearen Wachstumsprozessen ist traditionell im Lehrplan Mathematik der Jahrgangsstufe 10 (und natürlich der Sek.II) verankert und nimmt dort einen wichtigen Platz ein. Dabei beschränken sich die behandelten Problemstellungen i.d.R. auf eine Untersuchung exponentieller Wachstumsprozesse, d.h. solcher, die sich mathematisch mit Hilfe von Exponentialfunktionen beschreiben lassen. Betrachtet man die üblicherweise in den Mathematik-Schulbüchern zu findenden Aufgabenstellungen, so wird man häufig auch auf "Anwendungsprobleme" stoßen, denen das Modell des exponentiellen Wachstums mehr oder weniger unkritisch "übergestülpt" wird, obwohl es eigentlich gar nicht passend ist, da exponentielles Wachstum unbeschränkt ist, was reale Wachstumsprozesse jedoch in unserer begrenzten Welt naturgemäß nicht sein können.

Auch Hefekulturen wachsen

Ein schönes Beispiel für nichtlineares, aber offenbar beschränktes Wachstum findet man bei Hefekulturen, die Carlson schon 1913 mit großer Sorgfalt untersucht hat.

Seine Daten - vgl. Tab. 1 - gaben bereits damals Anlass, sich genauere Gedanken über die möglichst exakte mathematische Beschreibung eines solchen Wachstumsprozesses zu machen, und führten schließlich zum Modell des logistischen Wachstums, das sich anhand dieses Beispiels sehr gut auch von Schülerinnen und Schülern "nacherfinden" lässt .

Wertvolle Hilfe bei der Exploration der in Tab.1 vorliegenden Hefedaten leistet eine Tabellenkalkulation wie z.B. das hier benutzte und weit verbreitete Excel oder - aufgrund der meist größeren Flexibilität oft noch besser geeignet, jedoch an Schulen nur sehr selten vorhanden - ein spezielles Statistik-Tool wie z.B. WinStat, StatView, Statistica, Systat, .... .

Genaueres zu solchen Werkzeugen kann man z.B. erfahren bei Biehler (1992), Rach (1995),
in Biehlers Link-Sammlung ( http://www.mathematik.uni-kassel.de/didaktik/HomePersonal/biehler/home/),
in den learn:line-Arbeitsbereichen

• "Lernen mit Neuen Medien" (http://www.learn-line.nrw.de/angebote/neuemedien/)
• "Explorative Datenanalyse" (http:// www.learn-line.nrw.de/angebote/eda/)

sowie über eine Abfrage des

• Software- Dokumentations- und Informations-Systems SODIS (http://www.sodis.de)

Hefekulturen - Wachstum ohne Ende?

Ein erster Blick in die Carlson-Daten (Tab.1) zeigt: Die Hefekultur wächst über den gesamten Zeitraum der erfassten 18 Stunden.

Mit welchen "Faustskizzen" werden Schülerinnen und Schüler nach einem flüchtigen Blick in die Tabelle spontan dieses Wachstum visualisieren? Erkennen sie auf Anhieb und ohne Vorwarnung, dass hier kein unbeschränktes Wachstum vorliegt, oder skizzieren sie etwa exponentielles oder gar lineares Wachstum, weil sie nur die Daten der ersten Stunden beachtet haben? Schnell können sich so Ansatzpunkte zu einer ersten Erörterung des vorliegenden Wachstumsprozesses ergeben.

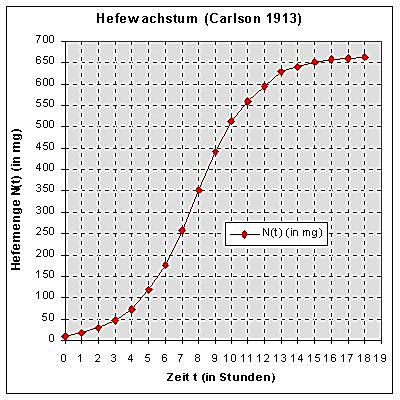
Einen guten Eindruck von der tatsächlichen Wachstumsart vermittelt dabei z.B. ein "professionelles" Liniendiagramm (Menge-Zeit-Diagramm, siehe Abb.1), das sowohl Tabellenkalkulationen als auch Statistik-Tools "auf Mausklick" erzeugen:

Abb. 1: Hefewachstum - Liniendiagramm

Dabei fällt sofort auf:

Nur in den ersten 8 Stunden scheint der Graph der Hefekultur N(t) etwa so wie der einer Exponentialfunktion zu verlaufen, danach "verflacht" er immer mehr.
Wagemutige könnten gar die Hypothese aufstellen, der Graph würde sich asymptotisch einer Parallele f(t)=K zur t-Achse mit 660 < K < 670 (mg) annähern, und sie könnten dieses K als "Kapazitätsgrenze" der Hefekultur interpretieren.

Die Untersuchung einer solchen Hypothese erfordert sicher eine genauere Analyse der Daten.

Dafür haben wir die Tab. 1 um einige abgeleitete Variablen erweitert:

Wir betrachten nun die 1-Stunden-Zeitintervalle, auf deren Mitten wir jeweils die "mittlere" Hefemenge Nm (t) in dieser Zeitspanne, die Hefezunahme in dieser Zeitspanne sowie die "Wachstumsproportion", also den Quotienten bezogen haben:

                     Tab. 2: erweiterte Tabelle

Wie ein erster Blick in die erweiterte Tabelle 2 zeigt, ist diese "Wachstumsproportion" auch schon in den ersten 8 Stunden keineswegs konstant, wie es bei einer Exponentialfunktion der Fall wäre, sondern sie ist von Anfang an "fast streng monoton fallend", bis schließlich nahezu Nullwachstum erreicht ist:

Das Hefewachstum ist also von Anfang an nicht exponentiell, sondern wird (nahezu) ständig und zunehmend stärker "abgebremst".

Das Modell des exponentiellen Wachstums passt schon in den ersten 8 Stunden nicht!

Aus diesen Beobachtungen ergeben sich für die weitere Datenexploration eine mathematische und eine biologische Frage:

1. mathematisch:
   Wie hängt die jeweilige Hefezunahme von der jeweils bereits
   erreichten Hefemenge Nm (t) ab, gibt es eine "Kapazitätsgrenze" K, und wie groß ist diese gegebenenfalls?
2. biologisch bzw. biochemisch:
   Wodurch wird eigentlich das Wachstum der Hefekultur so stark gebremst?

Auf mathematischer Entdeckungsreise !

Vielleicht kann ein Graph besser als die Zahlen Auskunft über die Abhängigkeit der Hefezunahme von der jeweils bereits erreichten mittleren Hefemenge Nm (t) geben?

Versuchsweise plotten wir gegen Nm (t) in einem Punktdiagramm (Abb.2):

Abb. 2: gegen Nm (t)

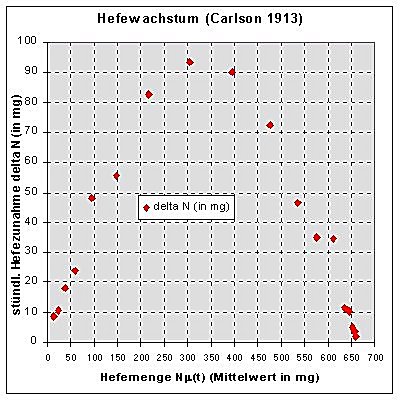
Die Entdeckung, dass dem S-förmigen Verlauf des Hefewachstums (Abb.1) ein solcher bogenförmiger Verlauf in der Abb.2 entspricht, dürfte die Mehrzahl der Schülerinnen und Schüler sicher überraschen! Kennen sie Funktionen, die zu einem solchen bogenförmigen Verlauf passen?

Vermutlich wird ihnen als erste (und evtl. auch einzige) eine quadratische Parabelfunktion einfallen, denn die Punkte ordnen sich in etwa auf einer nach unten geöffneten Parabel an, die durch den Nullpunkt und etwa durch den Punkt P(665/0) geht: Keine Hefemenge ( N(t)=0 ) bedeutet ebenso Nullwachstum wie die Hefemenge N(t)»665.

Schülerinnen und Schüler können zunächst versuchen, eine solche "Ausgleichsparabel" selbst nach Augenmaß in die Abb.2 einzutragen. Aber natürlich können sie nicht sicher sein, wirklich eine quadratische Parabel und nicht nur eine "Wunschkurve" gezeichnet zu haben.

Zur hier notwendigen Berechnung der Gleichung einer Ausgleichsparabel bieten sich z.B. folgende zwei Wege an:

Weg 1: Hand-Berechnung einer Ausgleichsparabel (vgl. Abb.3a)	Weg 2: Computerberechnung des Regressionspolynoms (vgl. Abb.3b)
Die Nullstellen x1 = 0 und x2 = K » 665 liefern die Gleichung	Die Nullstelle x1 = 0 liefert die Gleichung
Einsetzen des (mit maximalem D N=93,4) geschätzten Scheitelpunktes (oder alternativ eines charakteristisch erscheinenden Datenpunktes lt. Tab.2, natürlich mit abweichenden numerischen Ergebnissen) liefert die Parameter a » 0,000845 und c = a × K » 0,561805	Excel (o.a.) berechnet mit der Vorgabe der Nullstelle x1 = 0 aus allen Datenpunkten mit der "Methode der kleinsten Fehlerquadrate" die Parameter a » 0,000819 und c » 0,542837 Daraus ergibt sich als zweite Nullstelle x2 = K = a / c » 662,80

Zur Beschreibung der Abhängigkeit der Hefezunahme von der jeweils bereits erreichten mittleren Hefemenge Nm(t) erhält man auf diese Weise die Schätzgleichung

mit einem der oben ermittelten Parameter-Tripeln ( a, K, c ).

Die folgenden Abb.3a) und Abb.3b) zeigen für beide Wege die zugehörigen Plots.

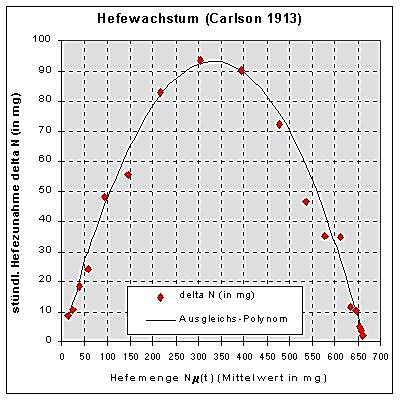
Abb.3a: Handberechnete Ausgleichsparabel	Abb.3b: Excels Regressionspolynom

                        
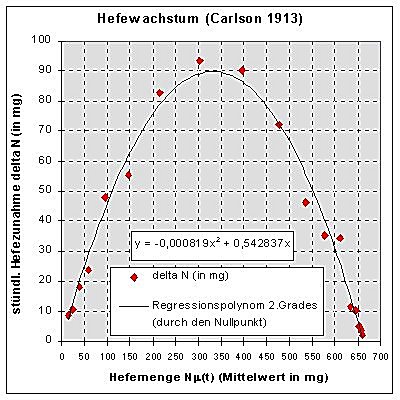Dabei scheint die handberechnete Ausgleichsparabel (Abb.3a) anschaulisch etwas besser zu den Datenpunkten zu passen, weil Excels Regressionspolynom in Scheitelpunktnähe stets unterhalb der Datenpunkte verläuft. Mehr Aufschluss über die Güte unserer "Fits" geben die zugehörigen Residuen-Plots (Abb.4a und Abb.4b), die übrigens bei Statistik-Tools i.d.Regel unmittelbar "auf Mausklick" verfügbar sind.

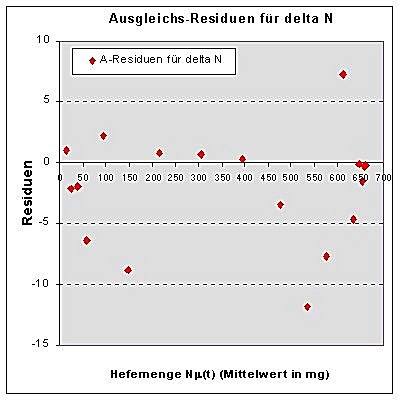
Abb.4a: Residuen zur hanberechneten Ausgleichsparabel	Abb.4b: Residuen zu Excels Regressionsploynom

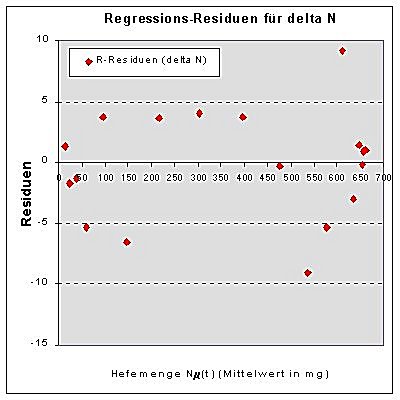Beide Residuen-Plots zeichnen sich durch ähnlich ungleichmäßige Charakteristiken der Residuen-Verteilungen aus. Dabei fällt auf, dass die Residuen in der Mitte eher positiv und an den Rändern eher negativ sind und dass die Residuen-Beträge bei der Ausgleichsparabel zwar in der Nähe des Scheitelpunktes kleiner, dafür aber links und rechts davon teilweise deutlich größer sind. Ob die Modelle wirklich brauchbar sind und welches Modell ggf. "besser" ist (evtl. gibt’s ja auch eine noch bessere Lösung), wollen wir durch einen Vergleich mit den ursprünglichen Daten ermitteln, den man z.B. auf einem der folgenden zwei Wege durchführen kann:

• Weg 1:
  Simulation mit einem Modellbildungs- und Simulationswerkzeug.
  Diesen Weg werden wir im übernächsten Abschnitt gehen.
• Weg 2:
  Sukzessive Berechnung der "gefitteten" N(t) aus den "gefitteten" D N(t)
  und aus N(0) = 9,6 und N(t) = N(t-1) + D N(t).
  Die Datei "hefe3.xls" auf der Begleitdiskette (im Verzeichnis "\logwachs\hefe") enthält solche Berechnungen, die wir hier aus Platzgründen nicht wiedergeben.

Verallgemeinerung zum Modell des logistischen Wachstums

Die Untersuchung zahlreicher Wachstumsprozesse (siehe den Absatz "Lust auf mehr?" am Ende des Artikels) führt immer wieder zu prinzipiell ähnlichen Ergebnissen.

Schülerinnen und Schüler können das am Beispiel der auf der Begleitdiskette vorliegenden Datensätze selbst erkunden und dabei das bisherige Vorgehen testen und reflektieren. Für den Fall, dass bei den vorliegenden Daten die Zeitspannen unterschiedlich lang bzw. ¹ 1 sind, müssen sie statt der einfachen Differenz DN(t) die jeweils durchschnittliche Zunahme je Zeiteinheit, also den Differenzenquotienten betrachten, der anschaulich als Sekantensteigung der Funktion N(t) interpretiert werden kann.

Sie werden feststellen:

Jeweils lässt sich die Abhängigkeit des durchschnittlichen Zuwachses vom in der betrachteten Zeitspanne durchschnittlich vorhandenen Wert N(t) mehr oder weniger gut beschreiben durch eine (diskrete) Differenzengleichung der Form

mit populationsspezifischen Werten für die Kapazitätsgrenze K und den Anpassungsfaktor a .

Formt man diese Differenzengleichung (*) ein wenig um zu

so kann man die Ähnlichkeit mit der bekannten Funktionalgleichung

des exponentiellen Wachstums gut erkennen: Bis auf einen "Korrekturfaktor" F(t) mit

stimmen beide Gleichungen überein! Dieser Korrekturfaktor F(t) ist offenbar für das "Bremsen" des Wachstums zuständig, während der jeweils konstante Faktor c = a× K als "anfängliche Wachstumsrate" von N gedeutet werden kann.

Wachstumsprozesse, die durch die Differenzengleichung (*) bzw. (**) charakterisierbar sind, werden allgemein als "logistisches Wachstum" bezeichnet, weil die wachsende Größe ihre Zunahme scheinbar mit einer gewissen "Logistik" steuert und abbremst, wenn ihre Existenzbedingungen zu schlecht werden. Auf diesem Gedanken beruht auch die Interpretation des Parameters K als "Kapazitätsgrenze". Charakteristisch für diese unterstellte "Logistik" sind die Eigenschaften (vgl. Abb.5) des Korrekturfaktors :

Abb.5: Eigenschaften des Korrekturfaktors F(t)

• Ist N(t) sehr viel kleiner als die "Kapazitätsgrenze" K, so ist F(t) » 1,
  d.h. es findet fast kein Bremsen statt.
• Ist N(t) » K , so ist F(t) » 0 ,
  d.h. es kommt zu einer sehr starken Bremswirkung, bis schließlich Nullwachstum eintritt.
• F(t) kann nur Werte zwischen 0 und 1 annehmen.
• Bei einer streng monoton steigenden Zustandsgröße N(t) ist F(t) streng monoton fallend.

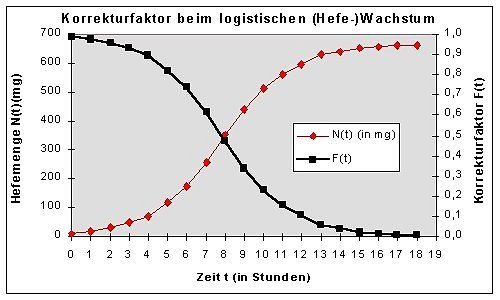
Ein Modell reizt zur Simulation ...

Kennt man die bestimmenden Parameter eines logistischen Wachstumsprozesses, nämlich

• Anfangswert N(0) der wachsenden Größe N
• Anpassungsfaktor a
• Kapazitätsgrenze K

so kann man diese Daten benutzen, um mit Hilfe eines Modellbildungswerkzeuges ein entsprechendes quantitatives Modell zu bauen und damit zu experimentieren.

Wir benutzen dazu das in Schulen weit verbreitete und sehr einfach zu bedienende DYNASYS, bauen mit "unseren" Parametern eine Modell-Hefekultur (vgl. Abb.6) und stellen für die Simulation das "Runge-Kutta-Verfahren" ein, da Hefe nicht diskret, sondern kontinuierlich wächst..

Abb.6: Dynasys-Modell zum Hefewachstum

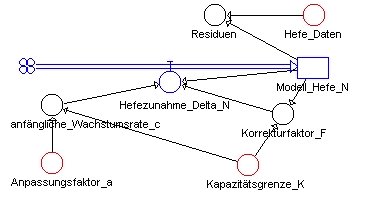
Das Modell ermöglicht einen Vergleich zwischen dem von Carlson beobachteten realen Hefewachstum und dem Wachstum unserer Modellhefe (vgl. Abb.7, Abb.8a und Abb.8b).

Abb.7: Dynasys-Simulation, Phasendiagramm
 

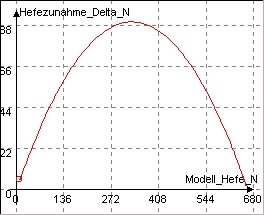
Das von DYNASYS erzeugte "Phasendiagramm" (Abb.7), das den Zusammenhang zwischen Modellhefe-Wachstum und Modellhefe-Größe veranschaulicht, entspricht dabei in etwa den aus den realen Daten gewonnenen Abb.3a und Abb.3b.

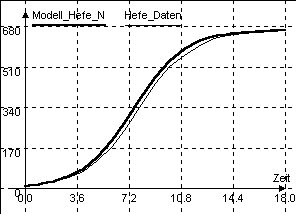
Abb.8a: Dynasys-Simulation zur Modellgüte               der handberechneten Ausgleichsparabel               mit a=0,000845 und K=665	Abb.8b: Dynasys-Simulation zur Modellgüte                des Regressionspolynoms                mit a=0,000819 und K=662,8

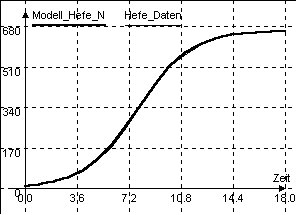Die Abb.8a und Abb.8b zeigen deutlich, dass die durch Regression gewonnenen Parameter zu einer sichtbar besseren Modellpassung führen als die durch Handberechnung der Ausgleichsparabel ermittelten. Im Regressions-Fall ist das Ergebnis hier sogar nahezu perfekt.

Dies belegen auch die kleinen zugehörigen Residuenbeträge in der Tab.3 recht deutlich.

Eine (wissenschaftlich nicht unumstrittene) Regression mit der "Methode der kleinsten Fehlerquadrate" wird allerdings nicht immer ein so gutes Resultat ergeben, und in der Tat kann man sogar bei unserem Hefebeispiel das Modell noch weiter verbessern. Z.B. liefern die experimentell ermittelten Modellparameter a=0,0008115 und K=665 noch etwas kleinere Residuen.

... und zum mathematischen Weiterdenken

Modellbildungssysteme wie DYNASYS lösen die diskrete Differenzengleichung

numerisch und benutzen zur Ermittlung von Werten der Funktion N(t) z.B. das Euler-Cauchy-Verfahren oder das Runge-Kutta-Verfahren. Lässt man jedoch im Sinne der Analysis D t beliebig klein werden, betrachtet also den Grenzwert , so wird aus der diskreten Differenzengleichung

die kontinuierliche Differentialgleichung

,

deren analytische Lösung

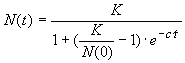
 wir hier allerdings lediglich der Vollständigkeit halber angeben.

 Und wer bremst nun das Hefewachstum?

Bevor es nun "zu" mathematisch wird, kommen wir lieber auf die zweite eingangs gestellte Frage zurück, nämlich der nach dem Verursacher der Wachstumsbremse. Schließlich wollen wir der Hefe keine eigene Intelligenz zusprechen, die sie tatsächlich zu logistischen Reaktionen auf ihre Lebensbedingungen befähigen würde.

Ausgehend von der Kenntnis der physiologischen Leistungsfähigkeit des Hefepilzes zur Alkohol-Produktion kann die Abb.9 den richtigen Gedankengang initiieren:

             Abb.9: (Quelle: Krebs 1984, S.217)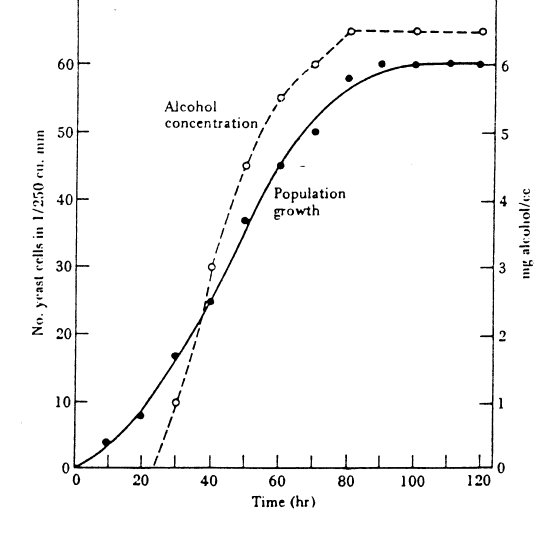

Beobachtung: Der Alkoholgehalt der Hefekultur steigt mit wachsender Hefemenge.

These: Der Alkohol bremst das Hefewachstum.

Bestätigung:
Schülerinnen und Schüler können diese These selbst experimentell bestätigen, wenn sie zu einer ursprünglich alkoholfreien Hefekultur nach und nach dosierte Alkoholmengen hinzufügen. Es empfiehlt sich für dieses Experiment allerdings eine Hefekultur zu nutzen, bei der der Pilz die Fähigkeit der Alkoholproduktion verloren hat. Normalerweise produziert die Hefe nämlich auch bei ausreichender Versorgung mit Sauerstoff Alkohol.

Anmerkungen:

1. Besonders motivierend wäre für eine Untersuchung des Hefewachstums im Rahmen eines fächerübergreifenden Unterrichtsprojekts sicherlich, wenn die Schülerinnen und Schüler - etwa in ihrem Biologie-Unterricht - selbst eine Hefekultur ansetzen und anstelle der Carlson-Daten die selbst erhobenen benutzen. Allerdings müssen die Daten dann sehr sorgfältig erhoben werden, und die Notwendigkeit, über einen längeren Zeitraum (etwa 18-24h) zumindest stündlich entsprechende Messungen durchzuführen, stellt sicher ein Hindernis für diese Vorgehensweise dar.
   Auswertungen der Entwicklung der Hefepopulation können mit einer Zählkammer erfolgen. Auf einem speziellen Objektträger mit einer feinen und definierten Vertiefung erfolgt die mikroskopische Auszählung der in dünner Schicht aufgetragenen Zellsuspension, die ein ganz bestimmtes Volumen einnimmt. Wer Messungen rund um die die Uhr vermeiden will, kann aus der wachsenden Kultur Proben ziehen und in ein Eisbad setzen, das das Wachstum stoppt. Gemessen werden können dann die Proben nach der Aufzucht.
2. Racke & Stein (1995) weisen darauf hin, dass es neben dem in diesem Artikel verfolgten logistischen Modellansatz (dessen wesentliches mathematisches Merkmal es ja ist, dass sich die Abhängigkeit der Zunahme der betrachteten Zustandsgröße von ihrem jeweils vorhandenen Wert durch eine quadratische Parabel beschreiben lässt, die durch den Ursprung geht), auch andere prinzipiell zu einem S-förmigen Wachstumsverlauf passende Modellansätze gibt.
   Jedoch sprechen gerade bei der Hefe biologische Gründe sehr stark für das logistische Wachstumsmodell:
   Bei Hefe begrenzt sich das Wachstum nämlich selbst und ohne zusätzliche Einwirkungen von außen, es handelt sich hier also tatsächlich um negative Rückkopplung - der von der Hefe bei ihrem Wachstum produzierte Alkohol hemmt seinerseits das Hefewachstum. Auch die Tatsache, dass mutierte Hefe, die keinen Alkohol produziert, ebenfalls nicht unbegrenzt wächst, stellt kein Gegenargument dar, sondern zeigt nur, dass es unterschiedliche wachstumshemmende "interne" Faktoren geben kann, die in der Biologie häufig unter dem Begriff "Stoffwechselreste" zusammengefasst werden, ohne dass man bisher genau weiß, was da eigentlich eine Rolle spielt.

 Literatur:

Biehler, R.:	Intendierte Anwendungen und didaktische Begründungen zu einem Softwarewerkzeug zur Explorativen Datenanalyse und stochastischen Simulation für Schule und Ausbildung, FWU, München 1992 (vergriffen, Restexemplare über den Autor erhältlich)
Biehler, R.:	Statistik-Links; http://www.mathematik.uni-kassel.de/didaktik/HomePersonal/biehler/home/
Goldkuhle,P., Kohorst, H., Portscheller,P.:	Arbeitsbereich "Modellierung und Simulation" , alte Adresse:http://www.learn-line.nrw.de/angebote/modell/index.html; neue Adresse: http://www.kohorst-lemgo.de/modell/index.html
Hupfeld, W.:	DYNASYS - Modellbildung und Simulation dynamischer Systeme, http://www.modsim.de/
IKARUS	Materialien zur Modellbildung und Simulation, http://www.ikarus.uni-dortmund.de/mediothek_modellbildung.html
Krebs, Ch.J.:	Ecology; The experimental analysis of distribution and abundance, New York 1972 (1.Auflage) und 1984 (3.Auflage)
Noll, G. Schmidt, G.:	Trends und Zusammenhänge, Materialien zur explorativen Datenanalyse und Statistik in der Schule, Soest 1994
Ogborn, J. Boohan, D.:	Making Sense of Data: Nuffield Exploratory Data Skills Project (9 Mini-courses with teacher booklets), London: Longman 1991
Pollok, B., Weinberg, P.:	learn:line-Arbeitsbereich "Explorative Datenanalyse", http://www.learn-line.nrw.de/angebote/eda/
Portscheller, P.:	learn:line-Arbeitsbereich "Lernen mit Neuen Medien", http://www.learn-line.nrw.de/angebote/neuemedien/
Rach, W.:	Softwarewerkzeuge für die Explorative Datenanalyse in der Schule, Computer und Unterricht, Jg.5, Heft 17/1995
Racke, U., Stein, G.:	Das logistische Wachstum als problematisches Beispiel mathematischer Modellbildung, ZDM 95/1
SODIS	Software- Dokumentations- und Informations- System, http://www.sodis.de
Winkelmann,B.:	Wachstum - Modellbildung und Simulation, Landesinstitut für Schule und Weiterbildung (Hrsg.), 1.Auflage (Entwurf), Soest 1992

Zusammenfassung

Schülerinnen und Schüler lernen im Mathematik-Unterricht ab Jgst.10 exponentielles Wachstum als ein Beispiel nichtlinearen Wachstums kennen und arbeiten dabei oft mit Daten, denen das Modell des exponentiellen Wachstums "fälschlich übergestülpt" ist, da reale Wachstumsprozesse in unserer begrenzten Welt naturgemäß nicht unbeschränkt sein können.

Am Beispiel der von Carlson 1913 erhobenen Daten zum Wachstum einer Hefekultur wird stattdessen ein elementarer Weg zum weit besser passenden Modell des logistischen Wachstums aufgezeigt: Die (hier mit Hilfe einer Tabellenkalkulation durchgeführte) Datenanalyse ergibt nämlich, dass sich die Abhängigkeit der Hefezunahme von der jeweils vorhandenen Hefemenge gut durch eine quadratische Parabel beschreiben lässt, deren Gleichung gerade der charakteristischen Differenzengleichung (bzw. Differentialgleichung) des logistischen Wachstums entspricht.

Mit Hilfe eines Modellbildungswerkzeuges wird dann die prinzipiell gute Passung des entwickelten logistischen Wachstumsmodells zu den Hefe-Daten festgestellt.

Schließlich wird aufgezeigt, wie Schülerinnen und Schüler auf experimentellem Wege feststellen können, dass nicht die Hefe selbst ihr eigenes Wachstum steuert, sondern dass die beim Hefewachstum zunehmende Alkoholkonzentration das Abbremsen des Hefewachstums verursacht.

Die mathematischen und die biologischen bzw. biochemischen Facetten der Thematik laden zu einem fächerübergreifenden oder fächerverbindenden Arbeiten ein.

Lust auf mehr? - Weitere Datensätze zur Modellierung logistischen Wachstums

Die Übertragbarkeit der am Hefe-Beispiel gewonnenen Beobachtung können (und sollten!) Schülerinnen und Schüler an weiteren auf der Begleitdiskette (im Verzeichnis "\logwachs") zusammengestellten kommentierten Datensätzen prüfen, zu denen sie eigene Explorationen und Modellbildungen durchführen.

Es ergeben sich dabei immer wieder Anlässe zu notwendigen kritischen Reflektionen:

Dass das Modell des logistischen Wachstums manchmal auch weniger gut zu den Daten passt, mindert allerdings nicht den Beschreibungs-, Erklärungs- und Prognosewert dieses Modells an sich, sondern kann und sollte jeweils dazu genutzt werden, die im Zuge eines Modellbildungsprozesses grundsätzlich notwendigen Abstraktionen zu reflektieren und die Aussagefähigkeit von Modellen überhaupt kritisch zu hinterfragen.

Festzuhalten ist: Das logistische Wachstumsmodell beschreibt nur recht allgemein ein (sanft) gebremstes Wachstum und wird daher stets nur ungefähr, aber nicht genau passen.

Anmerkungen zu den Datensätzen auf der Begleitdiskette

Datensatz 1: Sonnenblumenwachstum (Reed/Holland 1919)

Dieser Datensatz erfordert bei seiner Auswertung und beim "Überstülpen" des logistischen Wachstumsmodells eine durchaus kritische Betrachtungsweise:

Fraglich ist zunächst die Zuverlässigkeit der Daten insbesondere in den ersten Wochen der "Erhebung": die extreme Genauigkeit (auf 10tel mm!!) der hier angegebenen Höhen ist kaum glaubhaft!

Ferner passt dieses Modell erst in der zweiten Hälfte der "Beobachtungszeit" wirklich gut zu den erhobenen Daten. Ein plausibler Grund für die am Anfang größeren Abweichungen zwischen Modell und "Wirklichkeit" könnte z.B. in den konkreten Wetterbedingungen (Sonnenschein, Temperatur, Niederschlag) während der "Erhebungszeit" im Jahr 1919 liegen, doch dazu enthält der Datensatz leider keine Angaben.

Theoretisch möglich ist schließlich auch, dass bei "Beobachtungsbeginn" die Höhe schon einige cm betrug, oder dass Sonnenblumen grundsätzlich in den ersten Wochen schneller wachsen und daher vielleicht hier ein anderes Modell besser passen würde (vgl. auch den Datensatz zur Entwicklung der Weltbevölkerung).

Datensatz 2: Wachstum der Weltbevölkerung seit 1650 (Carr/Saunders; UN; DSW)

Der Datensatz legt eine zeitlich differenzierte Analyse nahe:

Bis zum 20.Jhdt. kann man mit guter Passung "exponentielles Wachstum",

seit etwa der Mitte des 20.Jhdts. dagegen "logistisches Wachstum" unterstellen, wobei sich anhand der Untersuchung eine Stabilisierung der Weltbevölkerung am Ende des 21.Jhdts. bei ca. 8,3 Mrd. prognostizieren lässt.

Diese möglichen "Ergebnisse" werfen gleich mehrere inhaltliche Fragen auf:

• Wer oder was führte zur Änderung des Wachstumsverhaltens in der Mitte des 20.Jhdts.?
  (Zunächst sprunghafte Wachstumsbeschleunigung als Folge des "Entwicklungshilfe"-Beginns 1950; vgl. auch Kohorst (1992, 1993))
• Wer oder was "bremst" eigentlich das Wachstum der Weltbevölkerung?
  (Übergreifen des "Demographischen Übergangs" auch auf "Entwicklungsländer", Familienplanung und sozioökonomische Entwicklung; vgl. auch Kohorst (1992, 1995))
• UN-Hochrechnungen gingen noch kürzlich davon aus, dass sich die Weltbevölkerung in der 2.Hälfte des 21.Jhdts. auf einem Niveau von 10-15 Mrd. (je nach Prognosevariante) stabilisieren wird. Welche anderen Daten benutzte die UN für ihre Prognosen, oder hat sich etwa jüngst der Wachstumsprozess so geändert, dass die hier vorliegenden Daten ein niedrigeres Stabilisierungsniveau erwarten lassen?
• Kann man ein Stabilisierungsniveau wirklich als "Kapazitätsgrenze" interpretieren?
  Ist nicht eine "Kapazitätsgrenze" lediglich eine unter bestimmten Randbedingungen konstante Grenze, die sich aber - hier je nach Produktionsmöglichkeiten und Konsumverhalten der Menschheit - durchaus verändern kann?

Datensatz 3: Wachstum von Pantoffeltierchen-Populationen in zwei Ansätzen (Gause 1934)
                       [Population 1]  und  [Population 2]

Die beiden Ansätze und die zugehörigen Daten zum Wachstum der Pantoffeltierchen entstammen den Versuchen von Gause, der die Pantoffeltierchen in Gefäßen mit Osterhauts Medium kultivierte, einer Salzmischung, die zwar für die Pantoffeltierchen bekömmlich ist, jedoch die Vermehrung der Bakterien, die das Futter der Pantoffeltierchen darstellten, unterbindet. Im zweiten Ansatz erhielten die Pantoffeltierchen jeweils die doppelte Futtermenge im Vergleich zum ersten Ansatz.. Auffällig ist das relativ starke Schwanken der Werte der Populationsentwicklung, für das folgende Erklärungen denkbar sind:

• Die Populationsdichte innerhalb des Kulturgefäßes, aus dem jeweils 0,5 ml einer Probe entnommen wurde, war etwas ungleichmäßig und spiegelt sich entsprechend in den Proben.
• Die Populationsdichte wurde zwar primär von der zugeführten Nahrung bestimmt, aber unvermeidliche Milieuschwankungen haben ebenfalls Einfluß auf die Vermehrungsrate, so daß die Daten etwas verrauscht sind.
• Die Vermehrung der Pantoffeltierchen erfolgt nicht völlig kontinuierlich, sondern in Teilschüben.

Akzeptiert man diese hypothetischen Faktoren, dann ist es legitim, zunächst die Daten mit einem Glättungsverfahren zu bearbeiten, um dann auf die geglätteten Daten das Modell des logistischen Wachstums anzuwenden. Sicherlich wird man aber die Legitimität dieses Verfahrens der doppelten mathematischen Modellierung diskutieren müsssen.

Literatur zu den Datensätzen:

Kohorst,H.:	Bevölkerungsexplosion, Materialien zur explorativen Datenanalyse und Statistik in der Schule, FWU, München 1992
Kohorst,H., Weber,W.:	Bevölkerungsexplosion, Computer und Unterricht, Jg.3, Heft 11/1993
Kohorst,H.:	Bevölkerungsprognosen, Computer und Unterricht, Jg.5, Heft 17/1995
Winkelmann,B.:	Wachstum - Modellbildung und Simulation, Landesinstitut für Schule und Weiterbildung (Hrsg.), 1.Auflage (Entwurf), Soest 1992

Haben Sie weitere interessante Datensätze zum Thema "Logistisches Wachstum"?
Über eine entsprechende Mitteilung würden wir uns sehr freuen!

eMail:   Helmut Kohorst   oder  Philipp Portscheller